Question

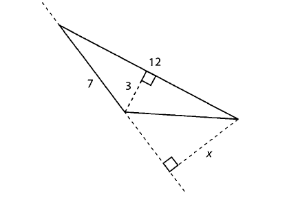
What is $ x $ in the figure below?

A. $ \dfrac{{22}}{7} $
B. $ \dfrac{{42}}{7} $
C. $ \dfrac{{36}}{7} $
D. $ 12 $

Answer 1

Hint: To find the value of $ x $ you can use the fact that area is always constant in triangles, it does not matter from what method or way we calculate it, we will always get the same value. So first find the area of the triangle taking $ 12 $ as base and $ 3 $ as its altitude. Then again this time take $ 7 $ as the base and $ x $ as its altitude and make an equation using the area of the triangle. And then solve the equation for the value of $ x. $
Formula used: Area of triangle: $ \dfrac{1}{2} \times b \times h,\;{\text{where}}\;b\;{\text{and}}\;h $ are lengths of base and height respectively.

Complete step-by-step answer:
In order to find the value of $ x $ in the given figure, we will see the figure closely, we observe that $ x $ is the exterior altitude of the triangle with sides $ 12\;{\text{and}}\;7 $ , so we can use this information to calculate its value.
Now, we know that $ x $ is the altitude of the triangle so we can derive an equation with help of the area of the triangle and for that we will first find area of the triangle as follows
 $ A = \dfrac{1}{2} \times 12 \times 3 = 18uni{t^2} $
If we take $ 7 $ as the base then $ x $ will be its respective altitude,
\[
   \Rightarrow A = \dfrac{1}{2} \times 7 \times x \\
   \Rightarrow 18 = \dfrac{1}{2} \times 7 \times x \\
   \Rightarrow 36 = 7 \times x \\
   \Rightarrow x = \dfrac{{36}}{7}units \;
 \]
Therefore length of \[x\;{\text{is}}\;\dfrac{{36}}{7}units.\]
So, the correct answer is “Option C”.

Note: There are two types of altitudes in a triangle interior altitude and exterior altitude. Generally students ignore the exterior altitude due to its less application, but you can see how exterior altitude helped us here in this question. So, always have all of your concepts clear so that you can solve this type of questions which are not directly formula based.