Question

X and Y are two stations which are 320 miles apart. A train starts at a certain time from X and travels towards Y at 70mph. After 2 hours, another train starts from Y and travels towards X at 20mph. At what time do they meet?
A. after 2 hours
B. after 3 hours
C. after 4 hours
D. after 5 hours

Answer 1

Hint: Given two stations are 320 miles apart. After two hours the first train travels some distance. Find this distance and subtract it from 320 miles. Now let the remaining distance be d. And let the time when the two trains meet be t. So the remaining distance d can be written as the sum of 70t and 20t. Equate the distance to this sum and find the value of t.

Complete step-by-step answer:
We are given that there are 2 stations X and Y which are 320 miles apart and a train starts at a certain time from X and travels towards Y at 70 miles per hour. After 2 hours, another train starts from Y towards X at 20 miles per hour.
We have to find the time when these two trains meet.
The first train starts from X towards Y. After 2 hours the distance travelled by 1st train is $2 \times 70 = 140$

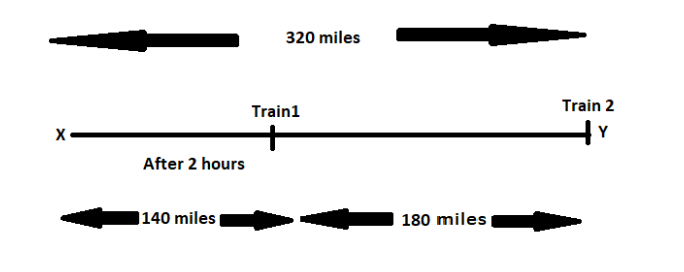
Distance travelled by the 1st train in 2nhours is 140 miles.
The remaining distance will be 320-140=180
After 2 hours the 2nd train starts at point Y towards X.
Let the time be t at which the two trains meet.
So the distance travelled by 1st train in t hours will be 70t miles and by 2nd train in t hours will be 20t miles and the distance travelled by both the trains in t hours will be 180.
$
  70t + 20t = 180miles \\
   \to 90t = 180 \\
   \to t = \dfrac{{180}}{{90}} \\
  \therefore t = 2hours \\
$
Therefore, the correct option is Option A, the two trains meet after 2 hours.
So, the correct answer is “Option A”.

Note: Here the speed of the 2nd train is much less than the speed of the 1st train and 2nd train might travel less distance compared to the 1st train because of its low speed. So the trains must meet in the leftover distance of 180 miles. Distance is the product of speed and time and that is what we have used in the above solution. 1 mile is not the same as 1 kilometre. Be careful with the units.