Question

\[x = 1\]is the radical axis of two circles which cut each other orthogonally. If \[{x^2} + {y^2} = 9\] is the equation of one circle, then the equation of the other circle is
A.\[{x^2} + {y^2} - 9x + 9 = 0\]
B.\[{x^2} + {y^2} + 18x - 9 = 0\]
C.\[{x^2} + {y^2} - 18x + 9 = 0\]
D.\[{x^2} + {y^2} + 9x + 9 = 0\]

Answer 1

Hint: Orthogonal circles cut one another at right angles. Using Pythagoras theorem, two circle of radii r1, r2 whose center are at distance d apart are orthogonal if \[r_1^2 + r_2^2 = {d^2}\] and given by the equation \[2gg' + 2ff' = c + c'\].
The angle of intersection of two overlapping circles is defined as the angle between their tangents at their intersection points. Where if the angle is \[{180^ \circ }\] it is known as tangent and the angle is \[{90^ \circ }\]then it is orthogonal.

Complete step-by-step answer:
Given the equation of one circle is \[{x^2} + {y^2} = 9\] whose center is (0, 0)

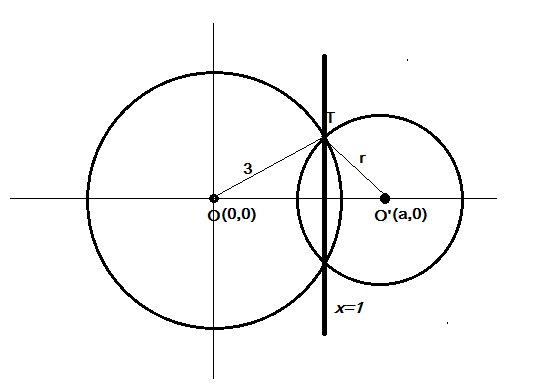
Given the radical axis of two circles\[x = 1\], therefore the line joining centers should be perpendicular to\[x = 1\]
The center of another circle should lie on\[y = 0\],
Let the center of another circle be \[\left( {a,0} \right)\]and the radius \[r\],
So the equation of other circle is \[{\left( {x - a} \right)^2} + {y^2} = {r^2} - - - - (i)\]
Since the given two circles are orthogonal we can write \[{a^2} = {r^2} + 9\]
We know the center of the two circle are at \[\left( {0,0} \right)\] and also their radius being 3 and r respectively
Since the lengths of the tangents from radial axis are equal, hence we get
\[\Rightarrow {\left( {1 - a} \right)^2} + 0 - {r^2} = 1 - 9\]
This can be written as:
\[
\Rightarrow {\left( {1 - a} \right)^2} + 0 - {r^2} = 1 - 9 \\
\Rightarrow 1 - 2a + {a^2} - {r^2} = - 8 \\
\Rightarrow {a^2} - {r^2} = 2a - 9 - - (i) \\
 \]
We know \[{a^2} = {r^2} + 9\] since the circles are orthogonal
\[\Rightarrow {a^2} - {r^2} = 9 - - (ii)\]
Hence by solving equation (i) and (ii) we can write
\[
\Rightarrow 2a - 9 = 9 \\
\Rightarrow 2a = 18 \\
\Rightarrow a = 9 \\
 \]
Also
\[
  {a^2} - {r^2} = 9 \\
\Rightarrow {\left( 9 \right)^2} - {r^2} = 9 \\
\Rightarrow {r^2} = 81 - 9 \\
\Rightarrow {r^2} = 72 \\
 \]
Substituting the values of $ a = 9 $ and $ {r^2} = 72 $ in equation (i) as:
\[
\Rightarrow {\left( {x - a} \right)^2} + {y^2} = {r^2} \\
\Rightarrow {\left( {x - 9} \right)^2} + {y^2} = 72 \\
\Rightarrow {x^2} + 81 - 18x + {y^2} - 72 = 0 \\
\Rightarrow {x^2} + {y^2} - 18x + 9 = 0 \\
 \]
Hence, the equation of the required circle is given as \[{x^2} + {y^2} - 18x + 9 = 0\].

So, the correct answer is “Option C”.

Note: Students must not get confused with the two equations of the circle as the coordinates of the center of both the circles are different. Moreover, the radius is varying by a considerable amount. Always try to stick to the fundamental standard equation of the circle i.e., $ {\left( {x - a} \right)^2} + {\left( {y - b} \right)^2} = {r^2} $ .