
What is wrong in this figure?
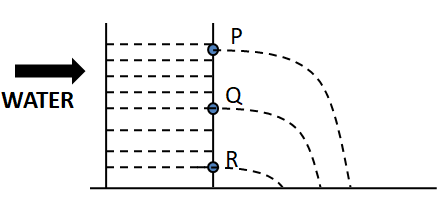
(A) Water flowing through-hole \[P\] will move a smaller distance as compared to \[Q\] and \[R\] .
(B) Water flowing through-hole ‘\[Q\]’ will be maximum.
(C) Water flowing through-hole ‘\[R\]’ will be more than ‘\[Q\]’ but less than ‘\[P\]’.
(D) Water flowing through all the holes will travel the same distance as pressure by a liquid is equal in all directions.

Answer
499.5k+ views
Hint: The question is based on the velocity of efflux of fluid. The pressures are defined for every hole according to the depths of the holes. Thereafter, The speed of water moving through the hole can be calculated by applying Torricelli’s law. Thereafter the comparison can be made by calculating the range of water flowing out.
Formula used:
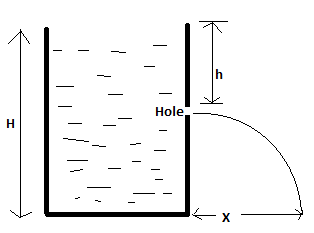
Let the total height of the container be\[H\] , and the height of the hole from the surface of the water level be\[h\] , then the height of the hole from the bottom of the container can be given as\[\left( {H - h} \right)\] . Hence the depth of the hole is \[\left( {H - h} \right)\]. So, the pressure at the point at which the hole is made, $P = (H - h)\rho g$.
$\rho $ is the density of the water and $g$ is the acceleration due to gravity.
If the velocity of the water flowing through the hole is $v$ , from Torricelli’s law $v \propto \dfrac{1}{P}$
Complete step by step solution:
If the total height of the container be\[H\], and \[h\] be the height of the hole from the surface of water level then the height of the hole from the bottom of the container is \[\left( {H - h} \right)\] ,
The given diagram is,
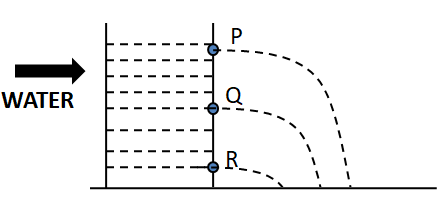
Let the heights of the holes from the surface of the water level be for holes\[P\] , \[Q\], and \[R\] be \[{h_P},{h_Q},{h_R}\] and, the displacements from the holes \[P\] , \[Q\], and \[R\]horizontally ${X_P},{X_Q},{X_R}$ respectively.
If the pressures at the holes \[P\] , \[Q\], and \[R\]be ${P_P}{\text{,}}{{\text{P}}_{\text{Q}}}{\text{,}}{{\text{P}}_R}$,
${P_p} = ({\text{H - }}{{\text{h}}_{\text{P}}}).\rho .g$
${P_Q} = ({\text{H - }}{{\text{h}}_{\text{Q}}}).\rho .g$
${P_R} = ({\text{H - }}{{\text{h}}_{\text{R}}}).\rho .g$
$\rho $ is the density of the water and $g$ is the acceleration due to gravity.
From Torricelli’s law we know that the pressure and velocity are in an inverse relationship, i.e. $v \propto \dfrac{1}{P}$. $v$ is the velocity of the water flowing through the hole.
Let the velocities of the water for holes\[P\] , \[Q\], and \[R\] be \[{v_P},{v_Q},{v_R}\]
Now by Mathematically comparing from the given diagram,
\[{h_R} > {h_Q} > {h_P}\]
$ \Rightarrow ({\text{H - }}{{\text{h}}_{\text{R}}}) < ({\text{H - }}{{\text{h}}_{\text{Q}}}) < ({\text{H - }}{{\text{h}}_{\text{P}}})$
$ \Rightarrow ({\text{H - }}{{\text{h}}_{\text{R}}}).\rho .g < ({\text{H - }}{{\text{h}}_{\text{Q}}}).\rho .g < ({\text{H - }}{{\text{h}}_{\text{P}}}).\rho .g$
$ \Rightarrow {P_R} < {{\text{P}}_{\text{Q}}} < {{\text{P}}_{\text{P}}}$
$ \Rightarrow {v_R} > {v_{\text{Q}}} > {v_{\text{P}}}$
$ \Rightarrow {X_R} > {X_Q} > {X_P}$ [since the displacement and velocity has a directly proportional relation]
From the above comparison, it is clear that water from the hole \[R\] will travel the farthest distance water from the hole $P$ will travel the smallest distance.
So, we can say that the Water flowing through-hole \[P\] will move a smaller distance as compared to \[Q\] and \[R\] as written in option (A).
Hence option A is the correct answer.
The figure given here is
It is wrong for the displacements of the water from the hole $P$ as well as \[R\]. Because $ {X_R} < {X_Q} < {X_P}$.
But it is given ${X_P} > {X_R}$ which is not correct.
Note:
With the help of the projectile motion the displacement of the water from a hole that is made is a certain height of the water-filled pot, can be formulated.
Let the total height of the container be\[H\] , and the height of the hole from the surface of the water level
be$h$ , then the height of the hole from the bottom of the container can be given as\[\left( {H - h} \right)\] . Now, let \[X\] be the distance traveled by the water flowing from the hole.
So the distance \[X\] can be given by the formula:-
\[X = 2\sqrt {h\left( {H - h} \right)} \].
Formula used:
Let the total height of the container be\[H\] , and the height of the hole from the surface of the water level be\[h\] , then the height of the hole from the bottom of the container can be given as\[\left( {H - h} \right)\] . Hence the depth of the hole is \[\left( {H - h} \right)\]. So, the pressure at the point at which the hole is made, $P = (H - h)\rho g$.
$\rho $ is the density of the water and $g$ is the acceleration due to gravity.
If the velocity of the water flowing through the hole is $v$ , from Torricelli’s law $v \propto \dfrac{1}{P}$
Complete step by step solution:
If the total height of the container be\[H\], and \[h\] be the height of the hole from the surface of water level then the height of the hole from the bottom of the container is \[\left( {H - h} \right)\] ,

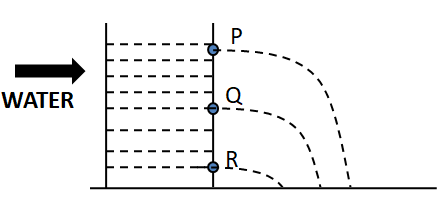
The given diagram is,

Let the heights of the holes from the surface of the water level be for holes\[P\] , \[Q\], and \[R\] be \[{h_P},{h_Q},{h_R}\] and, the displacements from the holes \[P\] , \[Q\], and \[R\]horizontally ${X_P},{X_Q},{X_R}$ respectively.
If the pressures at the holes \[P\] , \[Q\], and \[R\]be ${P_P}{\text{,}}{{\text{P}}_{\text{Q}}}{\text{,}}{{\text{P}}_R}$,
${P_p} = ({\text{H - }}{{\text{h}}_{\text{P}}}).\rho .g$
${P_Q} = ({\text{H - }}{{\text{h}}_{\text{Q}}}).\rho .g$
${P_R} = ({\text{H - }}{{\text{h}}_{\text{R}}}).\rho .g$
$\rho $ is the density of the water and $g$ is the acceleration due to gravity.
From Torricelli’s law we know that the pressure and velocity are in an inverse relationship, i.e. $v \propto \dfrac{1}{P}$. $v$ is the velocity of the water flowing through the hole.
Let the velocities of the water for holes\[P\] , \[Q\], and \[R\] be \[{v_P},{v_Q},{v_R}\]
Now by Mathematically comparing from the given diagram,
\[{h_R} > {h_Q} > {h_P}\]
$ \Rightarrow ({\text{H - }}{{\text{h}}_{\text{R}}}) < ({\text{H - }}{{\text{h}}_{\text{Q}}}) < ({\text{H - }}{{\text{h}}_{\text{P}}})$
$ \Rightarrow ({\text{H - }}{{\text{h}}_{\text{R}}}).\rho .g < ({\text{H - }}{{\text{h}}_{\text{Q}}}).\rho .g < ({\text{H - }}{{\text{h}}_{\text{P}}}).\rho .g$
$ \Rightarrow {P_R} < {{\text{P}}_{\text{Q}}} < {{\text{P}}_{\text{P}}}$
$ \Rightarrow {v_R} > {v_{\text{Q}}} > {v_{\text{P}}}$
$ \Rightarrow {X_R} > {X_Q} > {X_P}$ [since the displacement and velocity has a directly proportional relation]
From the above comparison, it is clear that water from the hole \[R\] will travel the farthest distance water from the hole $P$ will travel the smallest distance.
So, we can say that the Water flowing through-hole \[P\] will move a smaller distance as compared to \[Q\] and \[R\] as written in option (A).
Hence option A is the correct answer.
The figure given here is

It is wrong for the displacements of the water from the hole $P$ as well as \[R\]. Because $ {X_R} < {X_Q} < {X_P}$.
But it is given ${X_P} > {X_R}$ which is not correct.
Note:
With the help of the projectile motion the displacement of the water from a hole that is made is a certain height of the water-filled pot, can be formulated.
Let the total height of the container be\[H\] , and the height of the hole from the surface of the water level
be$h$ , then the height of the hole from the bottom of the container can be given as\[\left( {H - h} \right)\] . Now, let \[X\] be the distance traveled by the water flowing from the hole.
So the distance \[X\] can be given by the formula:-
\[X = 2\sqrt {h\left( {H - h} \right)} \].
Recently Updated Pages
Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Master Class 11 Biology: Engaging Questions & Answers for Success

Trending doubts
One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

There are 720 permutations of the digits 1 2 3 4 5 class 11 maths CBSE

Discuss the various forms of bacteria class 11 biology CBSE

Draw a diagram of a plant cell and label at least eight class 11 biology CBSE

State the laws of reflection of light

Explain zero factorial class 11 maths CBSE




