Question

Write two-two points of your choice which lie on X-axis and Y-axis.

Answer 1

Hint: For any point on X-axis, ordinate must be 0, and so the coordinates should be of the form (a,0). For any point on Y-axis, abscissa must be 0, and so the coordinates should be of the form (0,b). Hence, we can take any value for a and b to get the required points. Next, we can plot these points on the Cartesian coordinate.

Complete step by step solution:
We know that in a Cartesian coordinate system, two fixed lines are perpendicular to each other. This system can uniquely identify each point on the plane by a set of two coordinates, which are the distances of the point from the two fixed lines. We define the horizontal fixed line as the X-axis, and the vertical fixed line as the Y-axis.
We are well aware the any point P, on this Cartesian plane, will be of the form P (a,b). Here, we call a as the abscissa of point P, that represents the distance of point P from Y-axis. And, we call b as the ordinate of point P, that represents the distance of point P from X-axis.
We can very easily say that for any point on X-axis, the ordinate must be 0. Thus, we can say that any point of the form (a,0) will lie on the X-axis.
So, (1,0) and (-1,0) are two points on the X-axis. We can plot these points on the X-axis, as shown in red colour on the graph.
Similarly, we can say that for any point on Y-axis, the abscissa must be 0. Thus, we can say that any point of the form (0,b) will lie on the Y-axis.
So, (0,1) and (0,-1) are two points on the Y-axis. We can plot these points on the Y-axis, as shown in blue colour on the graph.

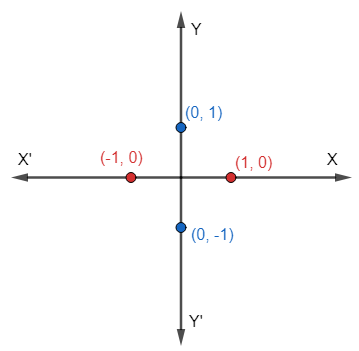
Hence, we can clearly see that, (1,0) and (-1,0) are two points on the X-axis, and (0,1) and (0,-1) are two points on the Y-axis as shown in the figure.

Note: We must take care that in a system of coordinates, the first term is abscissa and the second term is ordinary. Points with the coordinates of the form (a,0) lie on the X-axis, and the points with coordinates of the form (0,b) lie on the Y-axis. We must understand that is just a possible solution, and that this problem can have infinitely different solutions.