Question

Write the value of the given inverse trigonometric expression ${{\tan }^{-1}}\left( \tan \dfrac{3\pi }{4} \right)$.

Answer 1

Hint: For solving this question first, we will go through some important aspects like domain and range of the inverse trigonometric function $y={{\tan }^{-1}}x$ . First, we will use one of the basic formulas of the trigonometric ratio to write $\tan \dfrac{3\pi }{4}=-1$ in the given term. After that, we will use one of the basic formula of inverse trigonometric functions, i.e. ${{\tan }^{-1}}\left( -1 \right)=-\dfrac{\pi }{4}$ for giving the final answer for the question correctly.

Complete step-by-step solution -
Given:
We have to find the value of the following term:
${{\tan }^{-1}}\left( \tan \dfrac{3\pi }{4} \right)$
Now, before we proceed we should know about the inverse trigonometric function $y={{\tan }^{-1}}x$ . For more clarity look at the figure given below:

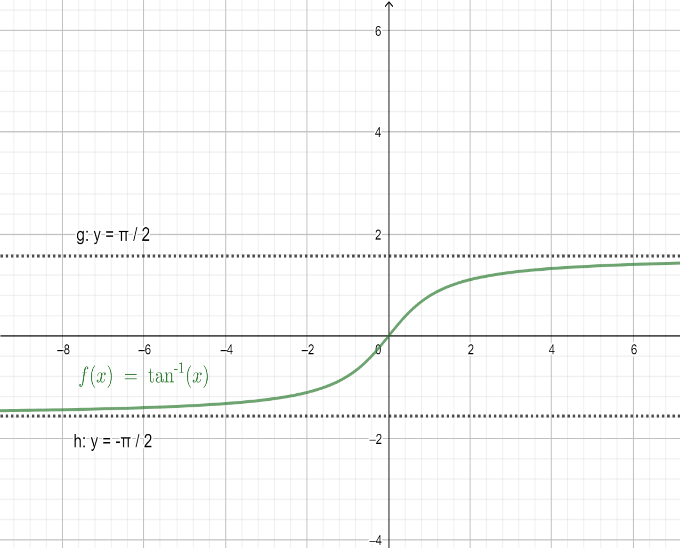
In the above figure, the plot $y=f\left( x \right)={{\tan }^{-1}}x$ is shown. And we should know that the function $y={{\tan }^{-1}}x$ is defined for $x\in \left( -\infty ,\infty \right)$ and its range is $y\in \left( -\dfrac{\pi }{2},\dfrac{\pi }{2} \right)$ .
Now, we will use the above concept for giving the correct value of ${{\tan }^{-1}}\left( \tan \dfrac{3\pi }{4} \right)$ .
Now, before we proceed further we should know the following formulas:
$\begin{align}
  & \tan \dfrac{3\pi }{4}=-1..................\left( 1 \right) \\
 & {{\tan }^{-1}}\left( -1 \right)=-\dfrac{\pi }{4}...........\left( 2 \right) \\
\end{align}$
Now, we will use the above two formulas to solve this question.
We have, ${{\tan }^{-1}}\left( \tan \dfrac{3\pi }{4} \right)$ .
Now, we will use the formula from the equation (1) to write $\tan \dfrac{3\pi }{4}=-1$ in the term ${{\tan }^{-1}}\left( \tan \dfrac{3\pi }{4} \right)$ . Then,
$\begin{align}
  & {{\tan }^{-1}}\left( \tan \dfrac{3\pi }{4} \right) \\
 & \Rightarrow {{\tan }^{-1}}\left( -1 \right) \\
\end{align}$
Now, we will use the formula from the equation (2) to write ${{\tan }^{-1}}\left( -1 \right)=-\dfrac{\pi }{4}$ in the above line. Then,
$\begin{align}
  & {{\tan }^{-1}}\left( -1 \right) \\
 & \Rightarrow -\dfrac{\pi }{4} \\
\end{align}$
Now, from the above result, we conclude that the value of the expression ${{\tan }^{-1}}\left( \tan \dfrac{3\pi }{4} \right)$ will be equal to $-\dfrac{\pi }{4}$ . Then,
${{\tan }^{-1}}\left( \tan \dfrac{3\pi }{4} \right)=-\dfrac{\pi }{4}$
Now, as it is evident that $-\dfrac{\pi }{4}$ lies in the range of the function $y={{\tan }^{-1}}x$ so, value of ${{\tan }^{-1}}\left( \tan \dfrac{3\pi }{4} \right)=-\dfrac{\pi }{4}$ .
Thus, ${{\tan }^{-1}}\left( \tan \dfrac{3\pi }{4} \right)=-\dfrac{\pi }{4}$.

Note: Here, the student should first understand what is asked in the question and then proceed in the right direction to get the correct answer quickly. Moreover, we should avoid writing ${{\tan }^{-1}}\left( \tan \dfrac{3\pi }{4} \right)=\dfrac{3\pi }{4}$ directly and use the basic concepts of domain and range of the inverse trigonometric function $y={{\tan }^{-1}}x$ correctly. And after giving the final answer, we should check for the validity of our answer by checking whether it lies in the range of the function $y={{\tan }^{-1}}x$.