Question

Write the statement of basic proportionality theorem.

Answer 1

Hint: Basic Proportionality Theorem was given by the popular Greek Mathematician, Thales, hence it is also known as the Thales Theorem. According to the famous mathematician, Thales, the ratio of any two corresponding sides will always be the same, for any two equiangular triangles. Based on this result, the Basic Proportionality Theorem (BPT) was introduced. It shows the relationship between the sides of any two equiangular triangles.
The concept of Thales Theorem had been introduced in case of similar triangles. If the two given triangles are similar to each other, then;
Corresponding angles of both the triangles will be equal
Corresponding sides of both the triangles will be in proportion to each other.
This theorem, therefore, also helps us to understand the concept of similar triangles in a better way. Now, let us try to write and understand the statement of Basic Proportionality Theorem.

Complete step-by-step answer:
The Basic Proportionality Theorem states that “if a line is drawn parallel to one side of a triangle to intersect the other two sides in distinct points, then the other two sides are divided in the equal ratio.
For example, in the figure given below, line \[AB\]is drawn parallel to side \[BC\], such that it intersects the other two sides, \[XY\]and \[XZ\]. The Basic Proportionality Theorem implies the consequence as \[\dfrac{{XA}}{{AY}} = \dfrac{{XB}}{{BZ}}\].

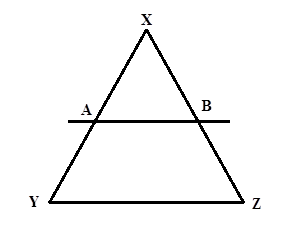
Note: Also, the converse of the Basic Proportionality Theorem holds true. According to the converse of the Basic Proportionality Theorem, “if a line segment intersects any two sides of a triangle in the equal ratio, then the line segment is parallel to the third side.”