Question

Write the reflection of point B (3, -4) in x-axis and y-axis.

Answer 1

Hint:
To find the reflection of a point along the x-axis, keep the abscissa constant and see the reflection of ordinate along the x-axis. Similarly, for the ordinate of the point.
Formula Used:
The reflection of point (x, y) along x axis is (x, -y)
And the reflection of this point along y axis is (-x, y)

Complete step by step solution:
We have to find the reflection of a given point along the x-axis as well as y-axis.
The given point is B (3, -4)
Now, to find the reflection of this point along the x-axis keep the abscissa constant and see the reflection of this point along the x-axis.
That is,

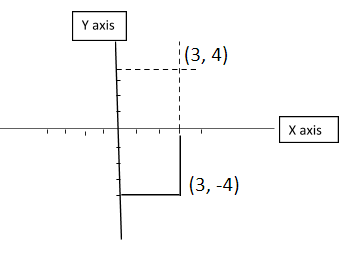
So, the reflection of point B (3, -4) along the x-axis is (3, 4).
Now we will see reflection point B (3, -4) along y-axis,
For this keep the ordinate constant and see the reflection of abscissa along y axis.
That is,

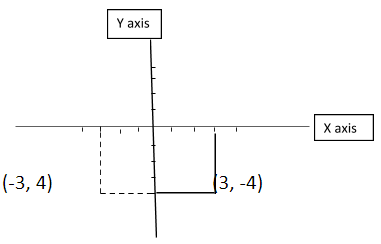
So, the reflection of point B (3, -4) along the y-axis is (-3, 4).

Additional Information:
Reflections in the coordinate plane:
Reflect over the x-axis: When you reflect a point across the x-axis, the x-coordinate remains the same, but the y-coordinate is transformed into its opposite (its sign is changed).
The reflection of the point (x, y) across the x-axis is the point (x, -y).


Reflect over the y axis: When you reflect a point across the y-axis, the y-coordinate remains the same, but the x-coordinate is transformed into its opposite (its sign is changed).
The reflection of the point (x, y) across the y-axis is the point (-x, y).
Reflect over the y=x: When you reflect a point across the line y=x, the coordinate and y-coordinate change places. If you reflect over the line y=-x, the coordinate and y-coordinate change places and are negated (the signs are changed).
The reflection of the point (x, y) across the line y=x is the point (y, x).
The reflection of the point (x, y) across the line y= -x is the point (-y, -x).

Note:
Reflection over the x-axis: When you reflect a point across the x-axis, the x-coordinate remains the same, but the y-coordinate is transformed into its opposite (its sign is changed).
The reflection of the point (x, y) across the x-axis is the point (x, -y).


Reflection over the y axis: When you reflect a point across the y-axis, the y-coordinate remains the same, but the x-coordinate is transformed into its opposite (its sign is changed).
The reflection of the point (x, y) across the y-axis is the point (-x, y).