Question

Write the ratio of radius to the diameter of a circle.
A. $\dfrac{1}{2}$
B. $\dfrac{1}{3}$
C. $\dfrac{{22}}{7}$
D. None of these.

Answer 1

Hint: The problem is to find the ratio of the radius to the diameter of a circle. To solve this, first of all, there should be a proper concept of radius and diameter and the knowledge of the relation between the radius and diameter of a circle. The radius of a circle is defined as the straight line starting from the centre of a circle to its perimeter. And the diameter of a circle is the line segment from one end of a centre from the other through its centre.

Complete step by step answer:
Basically, the length of the radius of a circle is the half of diameter of any circle. In other words, diameter is twice the length of radius of a circle.

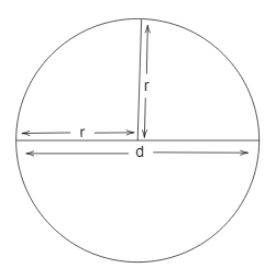
Let us assume, $r$ be the radius of a circle and $d$ be the diameter of the same circle. Then, clearly $d = 2r$. Now to find the ratio of radius to diameter, the required value of the ratio will be found by evaluating $\text{radius : diameter}$.
Hence the ratio= $\dfrac{\text{radius}}{\text{diameter}} = \dfrac{r}{d}$ … … …(i)
But $d = 2r$.
Putting the value of $d$ in (i)
$\text{ratio} = \dfrac{\text{radius}}{\text{diameter}} \\
\Rightarrow \text{ratio} = \dfrac{r}{d} \\
\Rightarrow \text{ratio} = \dfrac{r}{{2r}} \\
\therefore \text{ratio} = \dfrac{1}{2}$..............[cancelling $r$ from both numerator and denominator as $r \ne 0$].
Therefore, the required ratio of radius and diameter of a circle is $\dfrac{1}{2}$.

Hence option Ais correct.

Note: A circle is a bounded, curved shape, which is two-dimensional and all the points on it are equidistant to a particular point named as the centre. Another definition of a circle is the locus of a point in a plane, moving around such that the distance of each point from the particular fixed point is exactly the same. Other notable facts, radius and diameter of a circle are always unique and diameter will always be greater than the length of radius.