Question

Write the points of non-differentiability of $f(x) = \left| {\log \left| x \right|} \right|$.

Answer 1

Hint: Here, we will plot the graph of the given function and find the points which are non-differentiable i.e., the points where the curve is changing its definition.

Complete step-by-step answer:

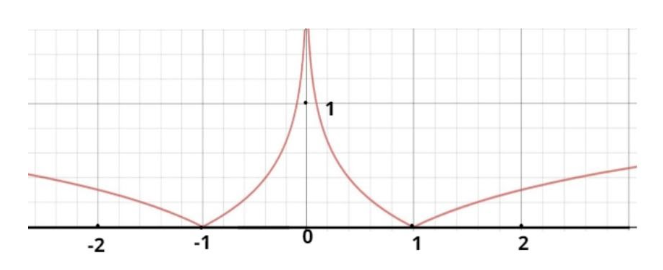
Now we have to find the points of non-differentiability of
$f(x) = \left| {\log \left| x \right|} \right|$
Now we know that the modulus function is an absolute function hence we can say that $f(x) = \left| {\log \left| x \right|} \right|$ will also be an absolute function
Now above graph depicts $f(x) = \left| {\log \left| x \right|} \right|$
Clearly we can see from the graph that our f(x) is continuous everywhere but however it is non-differentiable at points $x = - 1$ and $x = 1$ because the curve is changing its definition at these two depicted points.
Hence $x = \pm 1$ are the points where our $f(x) = \left| {\log \left| x \right|} \right|$ is non-differentiable.

Note: While solving such problems it is always advisable to have great knowledge of graphs as it helps saving a lot of time during solving a question in entrance exams.