
Write the pair of vertically opposite angles.

Answer
588k+ views
Hint:Vertical Angles are the angles opposite each other when two lines cross. "Vertical" in this case means they share the same Vertex (corner point).Using this definition we try to find vertical opposite angles from the figure.
Complete step-by-step answer:
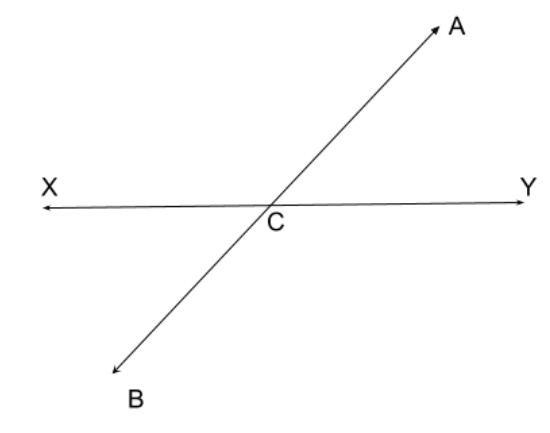
The given image is,
Vertical Angles are the angles opposite each other when two lines cross. "Vertical" in this case means they share the same Vertex (corner point).
Here \[AB\] and \[XY\] are two intersecting lines. They meet at \[C\].
Then the vertical angles are \[\angle ACY,{\text{ }}\angle XCB\,\&\, \angle XCA,{\text{ }}\angle BCY\]
The interesting thing here is that, vertical angles are equal.
So,
\[\angle ACY = \angle XCB\]
\[\angle XCA = \angle BCY\]
Thus we get, the pair of vertically opposite angles are \[\angle ACY,{\text{ }}\angle XCB\,\&\, \angle XCA,{\text{ }}\angle BCY\].
Note:When two lines intersect each other, then the opposite angles, formed due to intersection are called vertical angles or vertically opposite angles. A pair of vertically opposite angles are always equal to each other. Also, a vertical angle and its adjacent angle are supplementary angles, that is they add up to \[180^\circ \]. For example, if two lines intersect and make an angle, say \[X = 45^\circ \], then its opposite angle is also equal to \[45^\circ \]. And the angle adjacent to angle \[X\] will be equal to \[180^\circ - 45^\circ = 135^\circ \].
When two lines meet at a point in a plane, they are known as intersecting lines. When the lines do not meet at any point in a plane, they are called parallel lines.
Complete step-by-step answer:
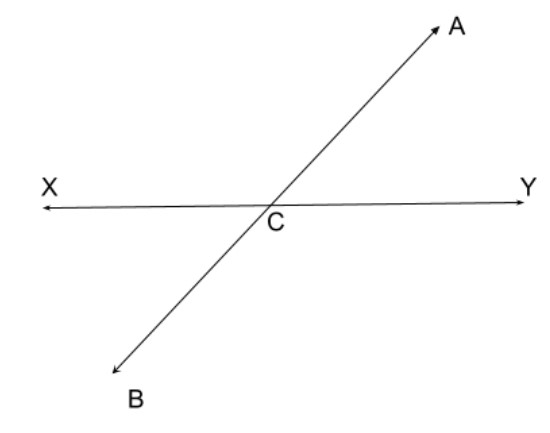
The given image is,

Vertical Angles are the angles opposite each other when two lines cross. "Vertical" in this case means they share the same Vertex (corner point).
Here \[AB\] and \[XY\] are two intersecting lines. They meet at \[C\].
Then the vertical angles are \[\angle ACY,{\text{ }}\angle XCB\,\&\, \angle XCA,{\text{ }}\angle BCY\]
The interesting thing here is that, vertical angles are equal.
So,
\[\angle ACY = \angle XCB\]
\[\angle XCA = \angle BCY\]
Thus we get, the pair of vertically opposite angles are \[\angle ACY,{\text{ }}\angle XCB\,\&\, \angle XCA,{\text{ }}\angle BCY\].
Note:When two lines intersect each other, then the opposite angles, formed due to intersection are called vertical angles or vertically opposite angles. A pair of vertically opposite angles are always equal to each other. Also, a vertical angle and its adjacent angle are supplementary angles, that is they add up to \[180^\circ \]. For example, if two lines intersect and make an angle, say \[X = 45^\circ \], then its opposite angle is also equal to \[45^\circ \]. And the angle adjacent to angle \[X\] will be equal to \[180^\circ - 45^\circ = 135^\circ \].
When two lines meet at a point in a plane, they are known as intersecting lines. When the lines do not meet at any point in a plane, they are called parallel lines.
Recently Updated Pages
Sam invested Rs15000 at 10 per annum for one year If class 8 maths CBSE

Magesh invested 5000 at 12 pa for one year If the interest class 8 maths CBSE

Arnavs father is 49 years old He is nine years older class 8 maths CBSE

2 pipes running together can fill a cistern in 6 minutes class 8 maths CBSE

If a man were to sell his handcart for Rs720 he would class 8 maths CBSE

By using the formula find the amount and compound interest class 8 maths CBSE

Trending doubts
Application to your principal for the character ce class 8 english CBSE

What are gulf countries and why they are called Gulf class 8 social science CBSE

Right to vote is a AFundamental Right BFundamental class 8 social science CBSE

What is the difference between rai and mustard see class 8 biology CBSE

Write a letter to the Municipal Commissioner to inform class 8 english CBSE

Find the simple interest on Rs 5000 for 2 years at class 8 maths CBSE




