Question

Write the lateral surface area of a cuboidal having length l units, breadth b units and height h units.
\[
  A.{\text{ }}2\left( {l + b} \right)h \\
  B.{\text{ }}2\left( {l + h} \right)b \\
  C.{\text{ }}3\left( {l + b} \right)h \\
  D.{\text{ }}2\left( {h + b} \right)l \\
 \]

Answer 1

Hint- In order to solve this question we will take an example of a room or a general cuboid and by considering its walls and base we will try to find out the lateral surface area of the cuboid.

Complete step-by-step answer:

We will use the following figure to solve the problem.

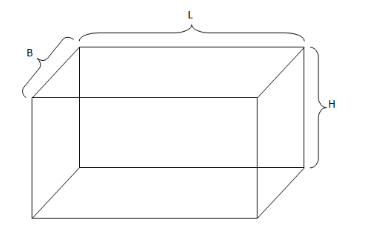
In order to find the lateral surface area of the cuboid we will find the area of the four walls of the cuboid.
The sides of front and the back walls of the cuboid are l units and h units.
So the area of front and back walls is $ = l \times h$
So the net area of front and back walls is $ = 2\left( {l \times h} \right)$
The sides of side walls of the cuboid are b units and h units.
So the area of side walls is $ = b \times h$
So the net area of side walls is $ = 2\left( {b \times h} \right)$
Therefore, the net lateral surface area = Area of front and back walls + area of side walls.
Net lateral surface area:
$
   = 2\left( {l \times h} \right) + 2\left( {b \times h} \right) \\
   = 2h\left( {l + b} \right) \\
   = 2\left( {l + b} \right)h \\
 $
Hence, the lateral surface area of the cuboid is $2\left( {l + b} \right)h$
So, option A is the correct option.

Note- This problem can be solved directly by the use of formula for the lateral surface area of the cuboids. But for better understanding the problem must be solved by the help of figures. The final solution obtained in the problem is the formula for lateral surface area of the cuboids and can be directly used in further problems.