Question

How do you write the inequality and solve given “two thirds of a number plus 5 is greater than 12?

Answer 1

Hint: In this particular problem, we not only translate the words into an algebraic expression but also find the inequality in the formed equation. We will also represent the inequality graphically. It also contains a symbol for inequality which is written in words as ‘greater than’. Expression will be formed using numbers and variables.

Complete step by step answer:
Now, let’s start solving the question. When we talk about algebraic expression, we usually come up with these three definitions: variable, coefficient and constant. Variable is just an alphabet whose value is not known to us. Coefficient is that constant value which is in product with the variable. For example: In 10z, 10 is a coefficient of ‘z’. And constant is a value which is alone in the expression and it is a number. For example: In 2y+8, 8 is a constant term.
Apart from algebraic expression, linear equations in one variable is also used. It means the equation which contains only a single variable. We call linear equality when there is an inequality like $>,<,\ge ,\le $ in linear equation having one variable. We represent that particular inequality in a graph by shaded portion and therefore it shows the data which is not equal. First, let’s translate the given words in algebraic expression then rest of the things will be after that.
First, let a number be ‘x’. if we say “two thirds of a number” it actually means the fraction $\dfrac{2}{3}$ is getting by a number which we have already assumed as ‘x’. So it will look like:
$\Rightarrow \dfrac{2}{3}\times x\Leftrightarrow \dfrac{2}{3}x$
After this, we have to perform addition as it’s written to add the above result with 5. So it will be:
$\Rightarrow \dfrac{2}{3}x+5$
Now this whole expression is greater than 12. We will write it as:
$\Rightarrow \dfrac{2}{3}x+5>12$
We got a linear equation finally.
For plotting the inequality, we need to follow some steps so that we can easily represent the equation on a graph. Step one is to rearrange the equation in such a way that the variable comes at the left and rest of the terms comes to the right. Next is to plot that equation on the graph. For example if an equation is given: $y\le 2x-1$. In this, we need to plot the line for y = 2x – 1. And further we have to shade the portion in which ‘y’ is less than 2x – 1.
So, next step is to solve for ‘x’. Take the like terms on one side:
$\Rightarrow \dfrac{2}{3}x>12-5$
$\Rightarrow \dfrac{2}{3}x>7$
Do reciprocal of $\dfrac{2}{3}$ and take it another side:
$\Rightarrow x>7\times \dfrac{3}{2}$
Multiply:
$\Rightarrow x>\dfrac{21}{2}$

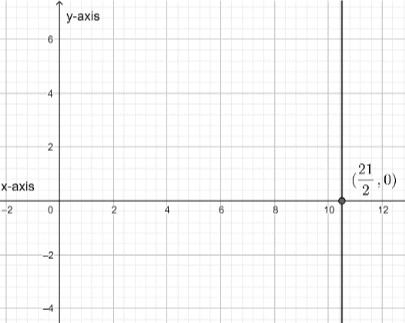
This graph is for x = $\dfrac{21}{2}$. This show the line without an inequality.

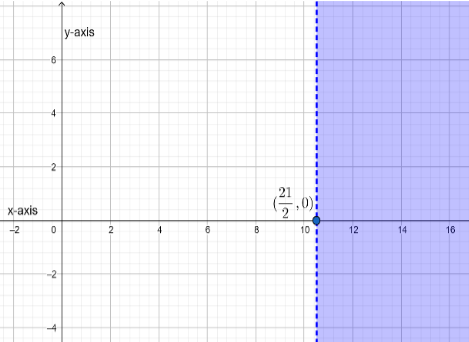
This is the graph of the inequality x < $\dfrac{21}{2}$. This inequality is represented by the shaded portion.

Note: This question is a combination of algebraic expression and solving inequalities. You can’t solve inequality directly without changing it into expression. For graphs are related to inequalities, you need to move step by step and don’t forget to shade the area covered under that equation.