Question

Write the formula of area and volume of different solid shapes. Find out the variables and constants in them.

Answer 1

Hint: By solid shapes in the question, it is referred to standard solid shapes, namely cylinder, sphere, cube, cuboid, cone. So, write the formulas for the total surface area, curved surface area and volume of all these solid shapes. Don’t forget to mention the meaning of different variables in each of the formulas.

Complete step by step answer:
In the above question, the term solid shapes refers to different standard solid shapes, namely cube, cuboid, cone, sphere, and cylinder. We need to write the formulas for the volume, total surface area and curved surface area for the following figures. We will also draw the figures for better understanding.
Let us start with a cube.

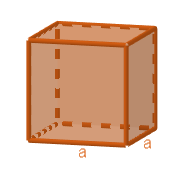
$\begin{align}
& \text{Volume}={{a}^{3}} \\
& \text{Total surface area}=6{{a}^{2}} \\
& \text{Curved surface area}=4{{a}^{2}} \\
\end{align}$
In the above formulas, ‘a’ is the length of each edge of the cube. In the above formulas 6 and 4 are the constants.

Now let us move to cuboid.

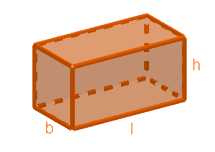
$\begin{align}
& \text{Volume}=l\times b\times h \\
& \text{Total surface area}=2\left( lb+bh+hl \right) \\
& \text{Curved surface area}=2\left( bh+hl \right) \\
\end{align}$
Here, l is the length, b is the breadth and h is the height of the cuboid. In the above formulas 2 is the constant,

Now, we will move to the cylinder.

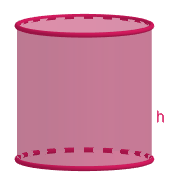
$\begin{align}
& \text{Volume}=\pi {{r}^{2}}h \\
& \text{Total surface area}=2\pi rh+2\pi {{r}^{2}} \\
& \text{Curved surface area}=2\pi rh \\
\end{align}$
In the above formulas, r is the radius of the circular ends and h is the height. Also, 2 and $\pi $ are constants and $\pi =3.14\text{ or }\dfrac{22}{7}$ .

Next, let us see the formulas for cones.

$\begin{align}
& \text{Volume}=\dfrac{1}{3}\pi {{r}^{2}}h \\
& \text{Total surface area}=\pi rl+\pi {{r}^{2}} \\
& \text{Curved surface area}=\pi rl \\
\end{align}$
In the above formulas, r is the radius of the circular end, l is the slant height and h is the height. Also, $\dfrac{1}{3}$ and $\pi $ are constants and $\pi =3.14\text{ or }\dfrac{22}{7}$ .

Finally, let us move to the sphere.

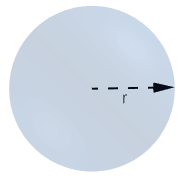
$\begin{gathered}
  {\text{Volume}} = \dfrac{4}{3}\pi {r^3} \\
  {\text{Total surface area}} = 4\pi {r^2} \\
  {\text{The curved surface area = }}4\pi {r^2} \\
\end{gathered} $
Here in the sphere the curved and total surface are equal because there is no plane surface area on the sphere.
In the above formula, r represents the radius of the solid sphere. Here, the constants are $4,3,\dfrac{4}{3}\text{ and }\pi $ .

Note: For solving the above question, it is necessary that you remember all the formulas related to curved surface area, total surface area and volume of each of the figures. Also, remember that all other polyhedrons are also included in the category of solid figures but are not standard solid figures, i.e., everything related to them is not a formula.