Question

Write the formula for the time period of a simple pendulum. On what factors it depends?

Answer 1

Hint:A simple pendulum is a point mass suspended from a fixed support and attached to a light inextensible cord. The mean position of a simple pendulum is the vertical line passing through the fixed support. The length of the simple pendulum, represented by \[L\] , is the vertical distance between the point of suspension and the suspended body's centre of mass (when it is in the mean position).

Complete step by step answer:
A simple pendulum is described as an item with a small mass, sometimes referred to as the pendulum bob, suspended from a light wire or string, as shown in Figure.

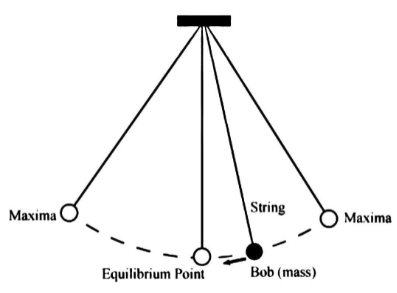
A simple pendulum's time period is given by:
$T = 2\pi \sqrt {\dfrac{l}{g}} $
Where, \[T = \] Time period, $\pi = pi = \dfrac{{22}}{7} = 3.14$, \[L = \] is the length of the pendulum and \[g = \] Gravitational acceleration.

The length of the pendulum, the acceleration due to gravity, and the temperature all affect the time period of a basic pendulum (as length depends on temperature). It has a direct relationship with the square root of length and an inverse relationship with the square root of gravity acceleration.

Note:When the temperature of a system varies, the simple pendulum's time period changes as the length of the pendulum changes. In a non-inertial frame of reference, a basic pendulum is suspended (accelerated lift, horizontally accelerated vehicle, vehicle moving along an inclined plane).