Question

Write the expression for velocity of a wave using the variables.

Answer 1

Hint : The velocity is the rate of change of displacement. The amplitude is $ x $ , wavelength is $ y $ and time period is $ z $ . So using these variables we can find the expression of the velocity of the wave.

Formula Used: The formulae used in the solution are given here.
 $ {\text{y = A sin}}\left( {\omega t - kx} \right) $ where $ y $ is the displacement, $ A $ is amplitude, the maximum displacement on either side, $ \omega $ is the angular frequency given by $ \dfrac{{2\pi }}{T} = 2\pi f $ where again, $ T $ is the time period and $ f $ is the frequency and $ k $ is a constant which is equal to $ \dfrac{{2\pi }}{\lambda } $ , where $ \lambda $ is the wavelength.

Complete step by step answer
A wave is produced when a vibrating source periodically disturbs the first particle of a medium. This creates a wave pattern that begins to travel along the medium from particle to particle. The frequency at which each individual particle vibrates is equal to the frequency at which the source vibrates. Similarly, the period of vibration of each individual particle in the medium is equal to the period of vibration of the source.
The equation of the wave is $ {\text{y = A sin}}\left( {\omega t - kx} \right) $ where $ y $ is the displacement, $ A $ is amplitude, the maximum displacement on either side, $ \omega $ is the angular frequency given by $ \dfrac{{2\pi }}{T} = 2\pi f $ where again, $ T $ is the time period and $ f $ is the frequency and $ k $ is a constant which is equal to $ \dfrac{{2\pi }}{\lambda } $ , where $ \lambda $ is the wavelength.
Velocity is the rate of change of displacement. It is given by calculating displacement per unit time.
Thus, velocity $ v = \dfrac{y}{t} $ where $ y $ is the displacement and $ t $ is the time taken.
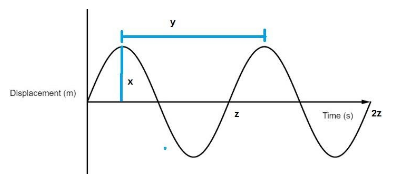
Here, $ T = z $ and $ \lambda = y $ and $ A = x $ .
Dividing both sides by $ z $ , we get,
 $ f'\left( x \right) = A\sin \left( {\dfrac{{2\pi t}}{z} - \dfrac{{2\pi }}{y}x} \right) $
So we can write,
 $ \Rightarrow f'\left( x \right) = A\cos \left( {\dfrac{{2\pi t}}{z} - \dfrac{{2\pi }}{y}} \right)x - \dfrac{{2\pi }}{y} $ .
Thus, the expression of wave v is:
 $ v = \dfrac{{ - 2\pi A}}{y}\cos 2\pi \left( {\dfrac{t}{z} - \dfrac{x}{y}} \right) $ .

Note
The wavelength is the period in space (aka the spatial period) of a waveform. It's the physical distance between one point on the wave and the next corresponding point. The frequency is the number of crests that pass a certain location in a given time. The crest is the peak part of the curve. The wave velocity is the velocity at which the shape of the wave propagates in space.
The velocity, frequency and wavelength of a wave are given by the formula:
Wave velocity ( $ v $ ) = frequency of waves ( $ f $ ) x wavelength of waves ( $ \lambda $ ).