Question

How do you write the equation of an ellipse in standard form given foci at \[( - 6,5)\] and $ ( - 6, - 7) $ and whose major axis has length 26?

Answer 1

Hint: In this question, we are given the coordinates of the foci and the length of the major axis of an ellipse and we have to find its equation. We will find the value of “a” by using the distance of the major axis and the value of “b” and the centre point by using the foci. Substituting the values in the standard form of an ellipse, we can find out the equation of the given ellipse.

Complete step by step solution:
The standard form of an ellipse is –
 $ \dfrac{{{{(y - k)}^2}}}{{{a^2}}} + \dfrac{{{{(x - h)}^2}}}{{{b^2}}} = 1 $
Where $ (h,k) $ is the coordinates of the centre of the ellipse, $ a $ is the length of the major axis and $ b $ is the length of the other axis.
The foci is written as \[F = (h,k + c)\] and $ F' = (h,k - c) $
We have $ F = ( - 6, - 7) $ and \[F' = ( - 6,5)\] so we get $ k + c = - 7 $ and $ k - c = 5 $
On adding the above two equations we get –
 $
  2k = - 2 \\
   \Rightarrow k = - 1 \;
  $
On putting the value of $ k $ in one of the two equations, we get $ c = -6 $ .
So, the centre of the ellipse is given as –
 $ \Rightarrow (h,k) = ( - 6, - 1) $
The major axis is the vertical axis, so –
\[
  2a = 26 \\
   \Rightarrow a = 13 \;
 \]
The length of the horizontal axis is $ 2c = 12 $
we take mod of value c as length cannot be negative,
Now, we know that
 $
  {a^2} - {b^2} = {c^2} \\
   \Rightarrow b = \sqrt {{{(13)}^2} - {{(6)}^2}} = \sqrt {169 - 36} = \sqrt {133} \;
  $
On putting all the values in the standard form, we get –
 $
  \dfrac{{{{[y - ( - 1)]}^2}}}{{{{(13)}^2}}} + \dfrac{{{{[x - ( - 6)]}^2}}}{{{{(\sqrt {133} )}^2}}} = 1 \\
   \Rightarrow \dfrac{{{{(y + 1)}^2}}}{{169}} + \dfrac{{{{(x + 6)}^2}}}{{133}} \;
  $
It can be graphed as –

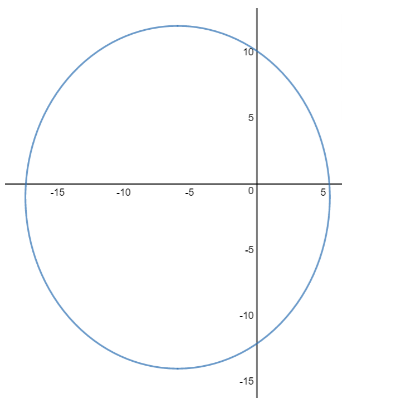
Note: An ellipse has 2 foci, and they help us find the axis on which or parallel to which the given ellipse has the major axis, as the x-coordinate of the foci of the given ellipse is the same, so it has a major axis on the vertical axis, that is, parallel to the y-axis. The coordinates of the centre of the ellipse can also be obtained by finding the midpoint of the foci.