Question

How do you write the equation of a line passing through \[( - 4, - 5)\] with slope \[ - \dfrac{3}{2}\] ?

Answer 1

Hint: When the coordinates of a point and the slope of the line is given, a point-slope form of the line is used, which is as mentioned below.
\[y - {y_1} = m(x - {x_1})\]

Complete step-by-step solution:
If the slope and a pair of points through which the line is passing are given in the question and one has to find the equation of such a line, we use the point-slope form of a line to obtain the equation.
The point-slope form is \[y - {y_1} = m(x - {x_1})\] , where \[{x_1}\] and \[{y_1}\] are the coordinates of the point through which the line is passing and \[m\] is the slope of the line.
In this case, \[{x_1} = - 4\,\] and \[{y_1} = - 5\] and \[m = - \dfrac{3}{2}\]
So, substituting these coordinates and value of slope in the equation we get
\[y - ( - 5) = - \dfrac{3}{2}(x - ( - 4))\]
Opening the brackets
\[ \Rightarrow (y + 5) = - \dfrac{3}{2}(x + 4)\]
Sending the denominator to the other side, we get,
\[ \Rightarrow 2(y + 5) = - 3(x + 4)\]
Opening the brackets and simplifying,
\[ \Rightarrow 2y + 10 = - 3x - 12\]
Keeping the constants on one side,
\[ \Rightarrow 2y = - 3x - 12 - 10\]
Further simplifying,
\[ \Rightarrow 2y = - 3x - 22\]
Therefore, the required equation is \[2y = - 3x - 22\].
Plotting on the graph,

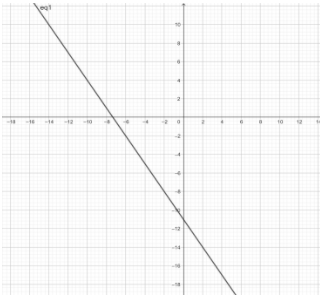
Note: The equation of a line is typically in the form of $y-mx+c$, where \[m\] is the slope of the line, \[c\] is the \[y\] -intercept of the line. This equation can be obtained and transformed to other forms, depending upon the quantities give in the equation.
In this question, slope and one point was given, hence we used point-slope form of the line, if, two points were given we would have used two-point form of the line, etc.
A common mistake while solving this equation occurs in the substitution of the given points in the equation. For example, in this question the given point is \[( - 4, - 5)\] , while putting this value make sure to substitute as \[y - ( - 5) = m(x - ( - 4)\] and not as \[ - 5 - y = m( - 4 - x)\] .