Question

How do you write the equation of a circle whose center is $\left( {3, - 2} \right)$ and a radius equal to $5$ units.

Answer 1

Hint: The given problem tests us on the concepts of coordinate geometry as well as conic sections. The problem requires us to find the equation of a circle given certain conditions. We first have to analyze the problem by drawing a figure for the situation and then plan our sequence of actions. We will substitute the value of radius and coordinates of the centre of the circle to obtain the equation of circle.

Complete step-by-step answer:
We are given the center of the circle as $\left( {3, - 2} \right)$.
Radius is also given to us as $5$ units.

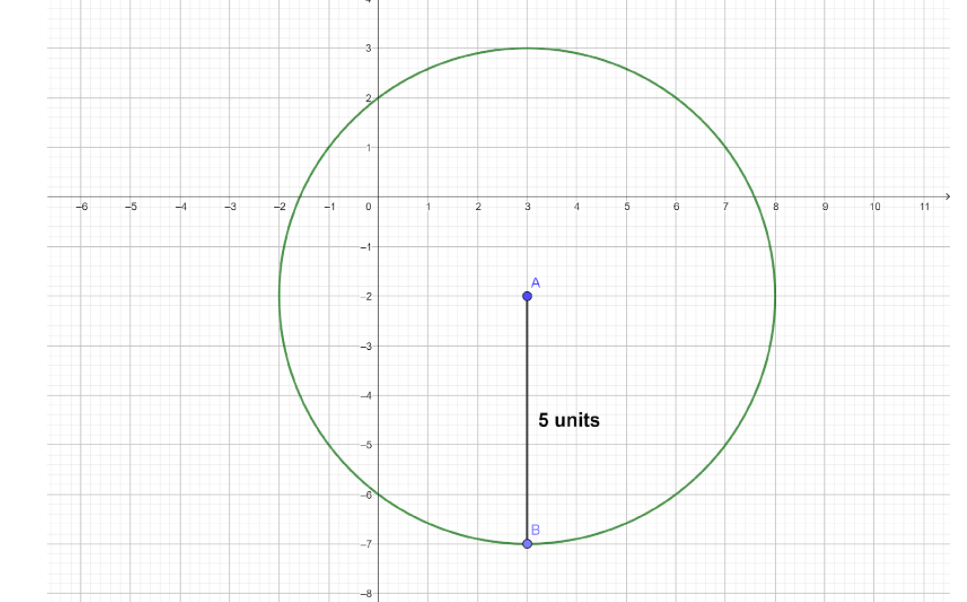
Now, we know that the standard equation of a circle whose centre is known to us as $\left( {\alpha ,\beta } \right)$ and the radius is r units is ${\left( {x - \alpha } \right)^2} + {\left( {y - \beta } \right)^2} = {r^2}$.
So, we know that the centre of the circle is $\left( {3, - 2} \right)$and the radius is $5$ units.
So, we get the equation of the circle as ${\left( {x - 3} \right)^2} + {\left( {y - \left( { - 2} \right)} \right)^2} = {\left( 5 \right)^2}$
Opening the brackets and simplifying the equation, we get,
$ \Rightarrow {\left( {x - 3} \right)^2} + {\left( {y + 2} \right)^2} = {\left( 5 \right)^2}$
Now, we know that the square of five is $25$. So, we get,
$ \Rightarrow {\left( {x - 3} \right)^2} + {\left( {y + 2} \right)^2} = 25$
So, the equation of the required circle whose center is $\left( { - 3,1} \right)$ and has a radius equal to $5$ units is ${\left( {x - 3} \right)^2} + {\left( {y + 2} \right)^2} = 25$.
So, the correct answer is “ ${\left( {x - 3} \right)^2} + {\left( {y + 2} \right)^2} = 25$”.

Note: Radius of a circle is the line segment joining any point on the circumference of the circle to the center of the circle. We can also expand the required equation of circle ${\left( {x - 3} \right)^2} + {\left( {y + 2} \right)^2} = 25$ by expanding the whole square terms using algebraic identities such as ${\left( {a - b} \right)^2} = {a^2} - 2ab + {b^2}$ and ${\left( {a + b} \right)^2} = {a^2} + 2ab + {b^2}$.
So, we have, ${\left( {x - 3} \right)^2} + {\left( {y + 2} \right)^2} = 25$
\[ \Rightarrow {x^2} - 6x + {3^2} + {y^2} + 4y + {2^2} = 25\]
Computing the squares, we get,
\[ \Rightarrow {x^2} - 6x + {y^2} + 4y = 12\]
So, we get the final equation as \[{x^2} - 6x + {y^2} + 4y = 12\].