
Write the decimal representation of $\dfrac{7}{8}$ .
Answer
569.4k+ views
Hint: We will find such a number that gives us such digits in the denominator which are integral powers of $10$ like$10,100,1000,...$ because this will make it easier to do the calculation. So multiply the numerator and denominator with such a number then place the decimal point before the number of digits counting from right to left) the same as the number of zeroes present in the denominator digit.
Complete step-by-step answer:
We have to write the given fraction into a decimal.
Here we will try to make the denominator such a number that it becomes easy for us to do the division. So, if we multiply such a number that the denominator becomes $100$ or $1000$ then it will make the calculation easier for us.
We know that $8 \times 125 = 1000$ so we will multiply the numerator and denominator with $125$. Then we get-
$ \Rightarrow \dfrac{7}{8} \times \dfrac{{25}}{{25}}$
On multiplication, we get-
$ \Rightarrow \dfrac{{875}}{{1000}}$
Now, to convert the given fraction into decimal we will place the decimal point before the number of digits the same as the number of zeroes present in the denominator digit. Since there are three zeroes in the denominator digit so we will place decimal point before three digits of the numerator counting from right to left-
$ \Rightarrow 0.875$
Hence the decimal representation of $\dfrac{7}{8}$ is $0.875$.
Note: Here we can also solve this question by directly dividing the numerator by denominator using the long division method. So we have to divide the numerator by denominator till we get the remainder as zero.
Since we can write $7$ as $7.000$ because the zeroes added after the decimal point do not change the value of the number, then divide the number by $8$. The division is shown below-
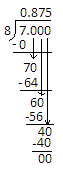
Complete step-by-step answer:
We have to write the given fraction into a decimal.
Here we will try to make the denominator such a number that it becomes easy for us to do the division. So, if we multiply such a number that the denominator becomes $100$ or $1000$ then it will make the calculation easier for us.
We know that $8 \times 125 = 1000$ so we will multiply the numerator and denominator with $125$. Then we get-
$ \Rightarrow \dfrac{7}{8} \times \dfrac{{25}}{{25}}$
On multiplication, we get-
$ \Rightarrow \dfrac{{875}}{{1000}}$
Now, to convert the given fraction into decimal we will place the decimal point before the number of digits the same as the number of zeroes present in the denominator digit. Since there are three zeroes in the denominator digit so we will place decimal point before three digits of the numerator counting from right to left-
$ \Rightarrow 0.875$
Hence the decimal representation of $\dfrac{7}{8}$ is $0.875$.
Note: Here we can also solve this question by directly dividing the numerator by denominator using the long division method. So we have to divide the numerator by denominator till we get the remainder as zero.
Since we can write $7$ as $7.000$ because the zeroes added after the decimal point do not change the value of the number, then divide the number by $8$. The division is shown below-
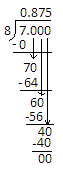
Recently Updated Pages
Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Master Class 11 Biology: Engaging Questions & Answers for Success

Master Class 11 Social Science: Engaging Questions & Answers for Success

Master Class 11 Physics: Engaging Questions & Answers for Success

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Trending doubts
What are the factors of 100 class 7 maths CBSE

The value of 6 more than 7 is A 1 B 1 C 13 D 13 class 7 maths CBSE

Full Form of IASDMIPSIFSIRSPOLICE class 7 social science CBSE

Convert 200 Million dollars in rupees class 7 maths CBSE

AIM To prepare stained temporary mount of onion peel class 7 biology CBSE

Write a letter to the editor of the national daily class 7 english CBSE





