Question

Write the coordinates of the image of A (-2, 5) under a translation $\left( {\begin{array}{*{20}{c}}
  4 \\
  { - 3}
\end{array}} \right)$.

Answer 1

Hint – In this particular type of question use the concept that in a translation i.e. $\left( {\begin{array}{*{20}{c}}
  4 \\
  { - 3}
\end{array}} \right)$, 4 belongs to the x-axis and (-3) belongs to the y-axis and use the concept that if the coordinate is positive than it moves to the positive direction and if the coordinates is negative than it moves towards the negative direction so use these concepts to reach the solution of the question.

Complete step by step answer:

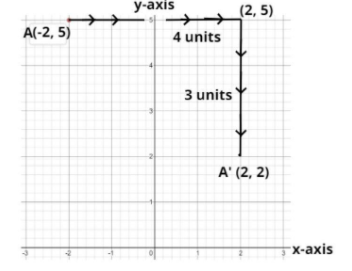
Although the answer is hidden in the figure which is A’ (2, 2)
But understand how it comes.
The point given is, A = (-2 , 5).
As the x coordinate is negative and the y coordinate is positive so the point A lie in the second quadrant as shown in the given figure.
Now we have to find the image of this point under the translation $\left( {\begin{array}{*{20}{c}}
  4 \\
  { - 3}
\end{array}} \right)$.
Its means that 4 units left from the point (as 4 is positive therefore it moves left side i.e. towards positive x axis) and from that point further moves (-3) units downwards (as -3 is a negative number therefore it moves downwards towards negative direction of y axis).
So after moving (+4) units left side form the point A (-2, 5) it reach to a point (2, 5) as shown in the figure, then it further moves from that point 3 units downward as shown in the figure and reach to a point A’ (2, 2) which is the required image of the point A under the translation $\left( {\begin{array}{*{20}{c}}
  4 \\
  { - 3}
\end{array}} \right)$.
So the image of the point A (-2, 5) is A’ (2, 2) under the translation $\left( {\begin{array}{*{20}{c}}
  4 \\
  { - 3}
\end{array}} \right)$ which lie in the first quadrant as shown in the figure.
So this is the required answer.

Note – Whenever we face such types of questions first check in which quadrant the given point lying then use the property of translation which is stated above and move the point A by 4 units left and then 3 units downwards to get the required image of the given point (A) under the translation $\left( {\begin{array}{*{20}{c}}
  4 \\
  { - 3}
\end{array}} \right)$ which comes out (2, 2), so this is the required answer.