Question

Write the coordinate of the vertices of a square whose, each side is 5 units, one vertex at $(2,1)$ and all the vertices lie in the same quadrant.

Answer 1

Hint: According to given in the question we have find all the remaining three vertices of the square when the coordinate of the vertices of a square whose, each side is 5 units, one vertex at $(2,1)$ and all the vertices lie in the same quadrant. So, first all we have to draw a quadrant of 2 planes having x-axis and y-axis now, we have to take measure or define the coordinates of each 1 unit as in the diagram given below:

Now, as given in the question we have to find the remaining three quadrants for square and as we know that in the square all the sides are equal to each other and all the interior angles of the square is ${90^\circ}$
Now, it is given that each side of square is 5 units and one of its vertex is at $(2,1)$ so, we have to plot the points $(2,1)$ on the quadrant where, we have to plot 2 units at the x-axis and 1 to the y-axis so with the help of this one vertex we can determine the other by forming the whole square in the quadrant.

Complete step-by-step answer:
Step 1: First of all we have to plot the one vertex which is $(2,1)$ on the quadrant having x-axis and y-axis and where, x-axis – 1units and y-axis- 1unit.

Step 2: Now, with the help of point A$(2,1)$ and as mentioned the square is of 5 units we can obtain the point B which is the vertex of the square. So, as we can that the B is at $(2,6)$ hence, another vertex is $(2,6)$ as mentioned in the figure below:

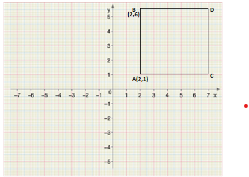
Step 3: Same as the step 2 we can obtain the coordinate of point C which is $(7,1)$ as mentioned in the figure below:

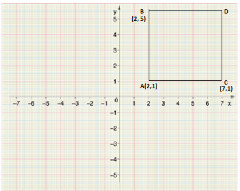
Step 4: Same as the step 3 we can obtain the coordinate of point C which is $(7,6)$as mentioned in the figure below:

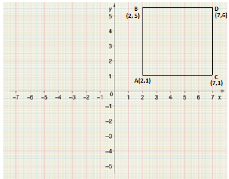
Hence with the help of quadrant we have obtained all the vertices of the square of side 5 units and one vertex is $(2,1)$ are $(2,6)$, $(7,1)$, and $(7,6)$.

Note: If one length of the side of a square is given then all the other sides will be equal to that given side because all the sides of a square are same or equal.
All the interior angles of the square are the same and are ${90^\circ}$ so there is no curve will be obtained while plotting the vertex of the square in the quadrant plane.