Question

Write the complex conjugate of 3 + 4i.

Answer 1

Hint: To solve this question, first of all, we will define what are complex numbers and what are its conjugates with their implications on the graph of the complex number and its conjugate in the complex plane. Then, with the concepts we have learned, we will find the conjugate of 3 + 4i.

Complete step-by-step answer:
A complex number is just addition of two parts, one real and imaginary, in the form a + ib. where, $ {{i}^{2}} $ = ─1. Since, this value of i doesn’t exist for any real number, mathematicians have defined complex numbers. The complex number a + ib has an imaginary part as well as a real part. a in the complex number a + ib is real whereas b in the complex number is an imaginary part. Either of a or b can be 0.
The conjugate of a complex number is also a complex number with the magnitudes of the real part and imaginary part as equal but the sign of the imaginary part is opposite.
Thus, the conjugate of a + ib will be a – ib.
Complex numbers can be plotted in the complex plane, with the horizontal axis as real part and vertical axis as imaginary part.
Thus, when we plot the complex number and its conjugate in the complex plane, they will be a mirror image about the real axis.
 

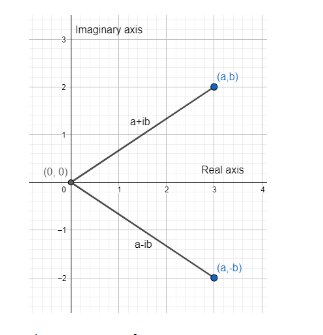
Thus, the conjugate of 3 + 4i is 3 – 4i.

Note: It is to be noted that every real number is a complex number with the imaginary part as 0, but the converse of this is not true, i.e. not all complex numbers are real numbers. We can write conjugates of a complex number just by changing the sign of the imaginary part.