Question

Write the associative law of addition of vectors.

Answer 1

Hint: Let us prove the associative law of addition of vectors by using a parallelogram with its sides as different vectors.

Complete step-by-step answer:

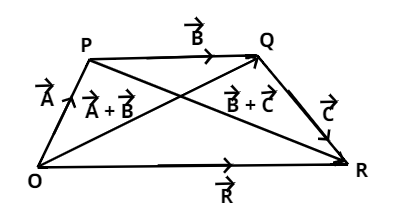
Now as we know that the associative law of addition of vectors states that the sum of the vectors remains same irrespective of their order or grouping in which they are arranged.
Like if \[\overrightarrow {\text{X}} \], \[\overrightarrow {\text{Y}} \] and \[\overrightarrow {\text{Z}} \] are the three vectors then according to associative law of addition of vectors \[\left( {\overrightarrow {\text{X}} {\text{ + }}\overrightarrow {\text{Y}} } \right){\text{ + }}\overrightarrow {\text{Z}} {\text{ = }}\overrightarrow {\text{X}} {\text{ + }}\left( {\overrightarrow {\text{Y}} {\text{ + }}\overrightarrow {\text{Z}} } \right)\]
As we know that according to head to tail rule if the head of one vector joins with the tail of another vector then the sum of both vectors will be the vector formed by the joining tail of one vector with the head of another.
So, now let \[\overrightarrow {\text{A}} \], \[\overrightarrow {\text{B}} \] and \[\overrightarrow {\text{C}} \] are the three vectors then applying head to tail rule to obtain the resultant of \[\overrightarrow {\text{A}} {\text{ + }}\overrightarrow {\text{B}} \] and \[\overrightarrow {\text{B}} {\text{ + }}\overrightarrow {\text{C}} \]
So, \[\overrightarrow {\text{A}} {\text{ + }}\overrightarrow {\text{B}} \] = \[\overrightarrow {{\text{OQ}}} \]
And, \[\overrightarrow {\text{B}} {\text{ + }}\overrightarrow {\text{C}} \] = \[\overrightarrow {{\text{PR}}} \]
Then finally again find the resultant of these three vectors,
So, \[\overrightarrow {{\text{OR}}} {\text{ = }}\overrightarrow {{\text{OP}}} {\text{ + }}\overrightarrow {{\text{PR}}} \]
Applying head to tail rule,
\[\overrightarrow {\text{R}} {\text{ = }}\overrightarrow {\text{A}} {\text{ + }}\left( {\overrightarrow {\text{B}} {\text{ + }}\overrightarrow {\text{C}} } \right)\] (1)
And, \[\overrightarrow {{\text{OR}}} {\text{ = }}\overrightarrow {{\text{OQ}}} {\text{ + }}\overrightarrow {{\text{QR}}} \]
Applying head to tail rule,
\[\overrightarrow {\text{R}} {\text{ = }}\left( {\overrightarrow {\text{A}} {\text{ + }}\overrightarrow {\text{B}} } \right){\text{ + }}\overrightarrow {\text{C}} {\text{ }}\] (2)
Thus, using equation 1 and 2. We can say that,
\[\left( {\overrightarrow {\text{A}} {\text{ + }}\overrightarrow {\text{B}} } \right){\text{ + }}\overrightarrow {\text{C}} {\text{ = }}\overrightarrow {\text{A}} {\text{ + }}\left( {\overrightarrow {\text{B}} {\text{ + }}\overrightarrow {\text{C}} } \right)\]
Hence, this fact is known as Associative law of vector addition.

Note: Whenever we come up with this type of problem then first, we assume that the three vectors as the sides of a parallelogram and then apply head to tail rule to find the sum of the vectors and this will prove the required result. And this will be the easiest and efficient way to prove the result.