Question

Write down the decimal expression of $\dfrac{{16}}{{3125}}$ without actual division.

Answer 1

Hint: To find the decimal expansion of a number without actually dividing the numbers, we will multiply both the numerators and denominators with a constant k. We will first find the value of k and then we will multiply such that the denominator becomes in the form of ${10^n}$ where n is an integer.

Complete step-by-step solution -
To solve the question we will multiply both the numerators and denominators with a constant k. The constant k should be such that when it is multiplied to the denominator, it is converted to the form ${10^n}$, where n is an integer. To find the value of k, first, we will find the prime factors of both the numerators and denominators. The prime factors of the numerator $\left( { = 16} \right)$ are:

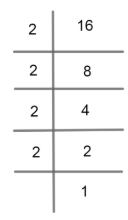
Thus, we can say that, $16 = 2 \times 2 \times 2 \times 2$. Now, we will calculate the prime factors of 3125:

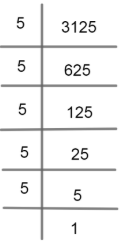
Thus, we can say that,
$3125 = 5 \times 5 \times 5 \times 5 \times 5$
Now, we will write $\dfrac{{16}}{{3125}}$ in the form of prime factors of numerator and denominator:
$\dfrac{{16}}{{3125}} = \dfrac{{2 \times 2 \times 2 \times 2}}{{5 \times 5 \times 5 \times 5 \times 5}}$
Now, in the denominator we have five 5s. If we multiply each 5 by 2 then it will become 10 and the denominator will be changed into a power of 10. Thus, we will multiply the denominator by $2 \times 2 \times 2 \times 2 \times 2$. We will also multiply the same to the numerator so that the value of the fraction remains the same. Thus, after multiplication, we get the following:
$ \Rightarrow \dfrac{{16}}{{3125}} = \dfrac{{2 \times 2 \times 2 \times 2}}{{5 \times 5 \times 5 \times 5 \times 5}} \times \dfrac{{2 \times 2 \times 2 \times 2 \times 2}}{{2 \times 2 \times 2 \times 2 \times 2}}$
$ \Rightarrow \dfrac{{16}}{{3125}} = \dfrac{{2 \times 2 \times 2 \times 2 \times 2 \times 2 \times 2 \times 2 \times 2}}{{5 \times 5 \times 5 \times 5 \times 5 \times 2 \times 2 \times 2 \times 2 \times 2}}$
$ \Rightarrow \dfrac{{16}}{{3125}} = \dfrac{{{2^9}}}{{10 \times 10 \times 10 \times 10 \times 10}}$
$ \Rightarrow \dfrac{{16}}{{3125}} = \dfrac{{{2^9}}}{{100000}}$
$ \Rightarrow \dfrac{{16}}{{3125}} = \dfrac{{512}}{{100000}}$
We know that $\dfrac{1}{{100000}} = 0.00001$
So, $\dfrac{{512}}{{100000}} = 512 \times \dfrac{1}{{100000}} = 512 \times 0.00001$
$ = 0.00512$
Thus, $\dfrac{{16}}{{3125}} = 0.00512$.

Note: We can use this method only when the denominator contains the power of 2 and 5 only. In case, if there is a power of some other prime number then this method will not be applicable.