Question

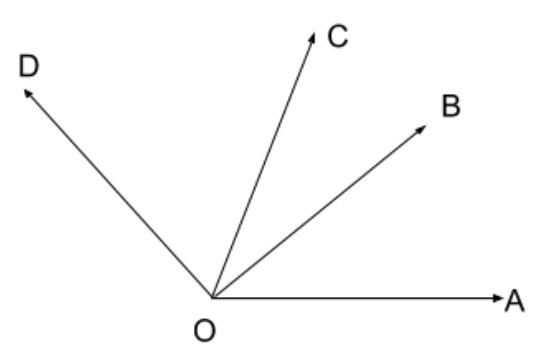
Write down each pair of adjacent angles shown in the figure.

Answer 1

Hint:Two angles are Adjacent when they have a common side and a common vertex (corner point) and don't overlap.Using this definition we try to find the adjacent angles.

Complete step-by-step answer:
The given image is,

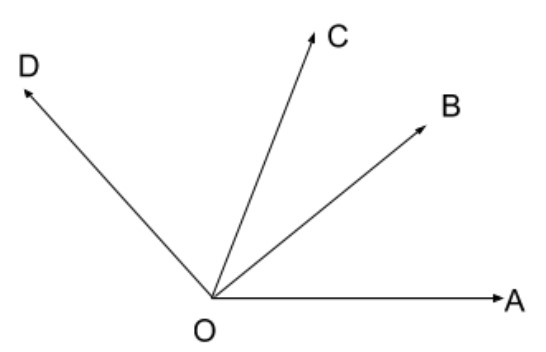
Two angles are Adjacent when they have a common side and a common vertex (corner point) and don't overlap.
Here\[\angle AOB\,\&\, \angle DOB\] are adjacent angles because
1) They have a common side \[OB\]
2) A common vertex \[O\] (corner point) and don't overlap.

Here\[\angle AOB\,\&\, \angle COB\] are adjacent angles because
1) They have a common side \[OB\]
2) A common vertex \[O\] (corner point) and don't overlap.

Here \[\angle AOC\,\&\, \angle COD\] are adjacent angles because
1) They have a common side \[OC\]
2) A common vertex \[O\] (corner point) and don't overlap.

Also we have,\[\angle COD\,\&\, \angle COB\] are adjacent angles because
1) They have a common side OC
2) A common vertex O (corner point) and don't overlap.
Thus we get, the each pair of adjacent angles are \[\angle AOB\,\&\, \angle DOB\], \[\angle AOB\,\&\, \angle COB\], \[\angle AOC\,\&\, \angle COD\], \[\angle COD\,\&\, \angle COB\].

Note:The two angles are said to be adjacent angles when they share the common vertex and side. The endpoints of the ray form the side of an angle is called the vertex of an angle. Adjacent angles can be a complementary angle or supplementary angle when they share the common vertex and side.
When two lines intersect each other, then the opposite angles, formed due to intersection are called vertical angles or vertically opposite angles. A pair of vertically opposite angles are always equal to each other. Also, a vertical angle and its adjacent angle are supplementary angles, that is they add up to \[180^\circ \]. For example, if two lines intersect and make an angle, say \[X = 45^\circ \], then its opposite angle is also equal to \[45^\circ \]. And the angle adjacent to angle \[X\]will be equal to \[180^\circ - 45^\circ = 135^\circ \].
When two lines meet at a point in a plane, they are known as intersecting lines. When the lines do not meet at any point in a plane, they are called parallel lines.