
How do you write $\dfrac{6}{{48}}$ as a decimal?
Answer
562.8k+ views
Hint: To convert a fractional value into a decimal, simply divide numerator by denominator. Hence, the numerator will be the dividend and the denominator will be the divisor. From this division, the quotient value obtained is the decimal value of the fractional number.
Complete step-by-step answer:
Firstly, let’s understand a fractional value and a decimal value.
In a fractional value, mostly the denominator of the fraction is considered as the whole body, and the numerator is considered as the part or share of the whole body.
Hence, generally, the numerator is smaller than or equal to the denominator.
In some cases, where the numerator is bigger than the denominator, it is considered as a whole body is already complete, considered as an integer and the remaining part is put in fractional value.
The decimal value shows a number that has an integer and the fractional part.
The decimal value has a decimal point, whose left-hand side shows the integer part and the right-hand side shows the fractional part.
To convert the fraction to decimal, divide the numerator by denominator. Hence, the numerator will be the dividend and the denominator will be the divisor.
From this division, the quotient value obtained is the decimal value of the fractional number.
Considering the question, we have $\dfrac{6}{{48}}$ .
We can reduce the fraction by factoring as shown
$ \Rightarrow \dfrac{6}{{48}} = \dfrac{6}{{6 \times 8}}$
Removing the common factor, we write the reduced fraction as
$ \Rightarrow \dfrac{6}{{48}} = \dfrac{1}{8}$
Now, for the decimal value, the numerator $\;1$ will be the dividend, and the denominator $\;8$ will be the divisor.
As the dividend is smaller than the divisor, we need to multiply $\;10$ to the dividend and add $\;0$ to the quotient.
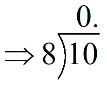
Now, applying simple division, we can find the quotient as below
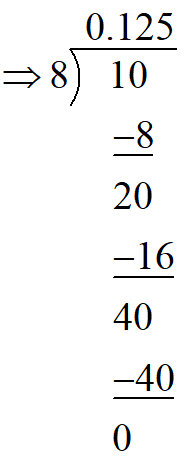
Hence, the quotient of the division is $\;0.125$ .
Hence, we can conclude that the decimal value for $\dfrac{6}{{48}}$ is $\;0.125$.
Note:
One can also try making the denominator a power of $\;10$ by multiplying the numerator and denominator with the same number. This process is done till the denominator is a power of $\;10$ and then the decimal value is obtained by adding the numerator on the right-hand side of the decimal point.
Complete step-by-step answer:
Firstly, let’s understand a fractional value and a decimal value.
In a fractional value, mostly the denominator of the fraction is considered as the whole body, and the numerator is considered as the part or share of the whole body.
Hence, generally, the numerator is smaller than or equal to the denominator.
In some cases, where the numerator is bigger than the denominator, it is considered as a whole body is already complete, considered as an integer and the remaining part is put in fractional value.
The decimal value shows a number that has an integer and the fractional part.
The decimal value has a decimal point, whose left-hand side shows the integer part and the right-hand side shows the fractional part.
To convert the fraction to decimal, divide the numerator by denominator. Hence, the numerator will be the dividend and the denominator will be the divisor.
From this division, the quotient value obtained is the decimal value of the fractional number.
Considering the question, we have $\dfrac{6}{{48}}$ .
We can reduce the fraction by factoring as shown
$ \Rightarrow \dfrac{6}{{48}} = \dfrac{6}{{6 \times 8}}$
Removing the common factor, we write the reduced fraction as
$ \Rightarrow \dfrac{6}{{48}} = \dfrac{1}{8}$
Now, for the decimal value, the numerator $\;1$ will be the dividend, and the denominator $\;8$ will be the divisor.
As the dividend is smaller than the divisor, we need to multiply $\;10$ to the dividend and add $\;0$ to the quotient.
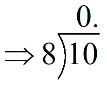
Now, applying simple division, we can find the quotient as below
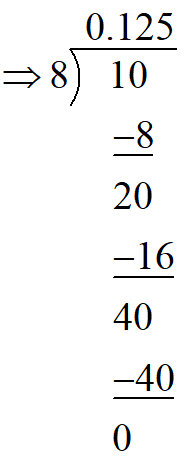
Hence, the quotient of the division is $\;0.125$ .
Hence, we can conclude that the decimal value for $\dfrac{6}{{48}}$ is $\;0.125$.
Note:
One can also try making the denominator a power of $\;10$ by multiplying the numerator and denominator with the same number. This process is done till the denominator is a power of $\;10$ and then the decimal value is obtained by adding the numerator on the right-hand side of the decimal point.
Recently Updated Pages
Master Class 10 Computer Science: Engaging Questions & Answers for Success

Master Class 10 General Knowledge: Engaging Questions & Answers for Success

Master Class 10 English: Engaging Questions & Answers for Success

Master Class 10 Social Science: Engaging Questions & Answers for Success

Master Class 10 Maths: Engaging Questions & Answers for Success

Master Class 10 Science: Engaging Questions & Answers for Success

Trending doubts
What is the median of the first 10 natural numbers class 10 maths CBSE

Which women's tennis player has 24 Grand Slam singles titles?

Who is the Brand Ambassador of Incredible India?

Why is there a time difference of about 5 hours between class 10 social science CBSE

Write a letter to the principal requesting him to grant class 10 english CBSE

A moving boat is observed from the top of a 150 m high class 10 maths CBSE




