
Write all the integers between \[ - 9\] and \[3\] which are odd.
Answer
592.8k+ views
Hint:We know that, Integers can be negative \[\left\{ { - 1,\, - 2,\, - 3,\; \ldots \ldots } \right\}\], positive \[\left\{ {1,{\text{ }}2,\,{\text{ }}3,{\text{ }}4,{\text{ }} \ldots \ldots } \right\}\] or zero\[\left\{ 0 \right\}\].Also we know that Odd numbers, when divided by \[2\], leave a remainder of \[1\]. So the odd integers are the positive or negative numbers which leave a remainder \[1\] when it is divided by \[2\].
Complete step-by-step answer:
We need to find out all the integers between \[ - 9\] and \[3\] which are odd.
We know that, Integers can be negative \[\left\{ { - 1,\, - 2,{\text{ }} - 3,\,{\text{ }} \ldots \ldots } \right\}\], positive \[\left\{ {1,{\text{ }}2,\,{\text{ }}3,{\text{ }}4,{\text{ }} \ldots \ldots } \right\}\] or zero\[\left\{ 0 \right\}\].
So the integers between \[ - 9\] and \[3\] are \[\left\{ { - 8,{\text{ }} - 7,\, - 6,{\text{ }} - 5,\; - 4,\; - 3,{\text{ }} - 2,\; - 1,\,0,{\text{ }}1,\,2} \right\}\]
Now we need to find out the odd numbers from the set \[\left\{ { - 8,{\text{ }} - 7,\, - 6,{\text{ }} - 5,\; - 4,\; - 3,{\text{ }} - 2,\; - 1,\,0,{\text{ }}1,\,2} \right\}\].
That is which leaves a remainder \[1\] when divided by \[2\].
That is the odd numbers from the set \[\left\{ { - 8,{\text{ }} - 7,\, - 6,{\text{ }} - 5,\; - 4,\; - 3,{\text{ }} - 2,\; - 1,\,0,{\text{ }}1,\,2} \right\}\] can be derived by finding the numbers which leave a remainder \[1\] when it is divided by \[2\].
They are \[ - 7,{\text{ }} - 5,\; - 3,\, - 1,\;1\].
Therefore all the integers between -9 and 3 which are odd are \[ - 7,{\text{ }} - 5,\; - 3,\, - 1,\;1\].
Note:
Whole numbers:
Whole numbers are simply the numbers in which zero is included \[0,{\text{ }}1,{\text{ }}2,{\text{ }}3,\;{\text{ }}4,\,{\text{ }}5,{\text{ }}6,{\text{ }} \ldots ..\]
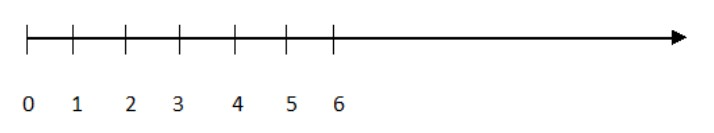
Integers:
Integers are like whole numbers, but they also include negative numbers but still no fractions allowed.
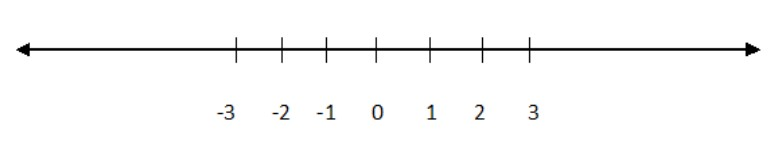
So integers can be negative \[\left\{ { - 1,{\text{ }} - 2,{\text{ }} - 3,\; \ldots \ldots } \right\}\], positive \[\left\{ {1,\,{\text{ }}2,\,{\text{ }}3,{\text{ }}4,{\text{ }} \ldots \ldots } \right\}\] or zero \[\left\{ 0 \right\}\].
Complete step-by-step answer:
We need to find out all the integers between \[ - 9\] and \[3\] which are odd.
We know that, Integers can be negative \[\left\{ { - 1,\, - 2,{\text{ }} - 3,\,{\text{ }} \ldots \ldots } \right\}\], positive \[\left\{ {1,{\text{ }}2,\,{\text{ }}3,{\text{ }}4,{\text{ }} \ldots \ldots } \right\}\] or zero\[\left\{ 0 \right\}\].
So the integers between \[ - 9\] and \[3\] are \[\left\{ { - 8,{\text{ }} - 7,\, - 6,{\text{ }} - 5,\; - 4,\; - 3,{\text{ }} - 2,\; - 1,\,0,{\text{ }}1,\,2} \right\}\]
Now we need to find out the odd numbers from the set \[\left\{ { - 8,{\text{ }} - 7,\, - 6,{\text{ }} - 5,\; - 4,\; - 3,{\text{ }} - 2,\; - 1,\,0,{\text{ }}1,\,2} \right\}\].
That is which leaves a remainder \[1\] when divided by \[2\].
That is the odd numbers from the set \[\left\{ { - 8,{\text{ }} - 7,\, - 6,{\text{ }} - 5,\; - 4,\; - 3,{\text{ }} - 2,\; - 1,\,0,{\text{ }}1,\,2} \right\}\] can be derived by finding the numbers which leave a remainder \[1\] when it is divided by \[2\].
They are \[ - 7,{\text{ }} - 5,\; - 3,\, - 1,\;1\].
Therefore all the integers between -9 and 3 which are odd are \[ - 7,{\text{ }} - 5,\; - 3,\, - 1,\;1\].
Note:
Whole numbers:
Whole numbers are simply the numbers in which zero is included \[0,{\text{ }}1,{\text{ }}2,{\text{ }}3,\;{\text{ }}4,\,{\text{ }}5,{\text{ }}6,{\text{ }} \ldots ..\]
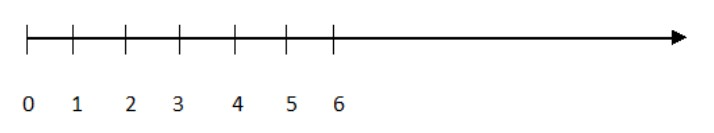
Integers:
Integers are like whole numbers, but they also include negative numbers but still no fractions allowed.

So integers can be negative \[\left\{ { - 1,{\text{ }} - 2,{\text{ }} - 3,\; \ldots \ldots } \right\}\], positive \[\left\{ {1,\,{\text{ }}2,\,{\text{ }}3,{\text{ }}4,{\text{ }} \ldots \ldots } \right\}\] or zero \[\left\{ 0 \right\}\].
Recently Updated Pages
Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Master Class 11 Biology: Engaging Questions & Answers for Success

Master Class 11 Social Science: Engaging Questions & Answers for Success

Master Class 11 Physics: Engaging Questions & Answers for Success

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Trending doubts
What is BLO What is the full form of BLO class 8 social science CBSE

Citizens of India can vote at the age of A 18 years class 8 social science CBSE

Full form of STD, ISD and PCO

Convert 40circ C to Fahrenheit A 104circ F B 107circ class 8 maths CBSE

Advantages and disadvantages of science

Right to vote is a AFundamental Right BFundamental class 8 social science CBSE





