Question

How do you write a quadratic equation with Vertex \[(5,5)\] and Point \[(6,6)\] ?

Answer 1

Hint: Just as a quadratic equation can map a parabola, the parabola's points can help write a corresponding quadratic equation. Parabolas have two equation forms – standard and vertex. The vertex of a parabola is the point at the top or bottom of the parabola. Vertex form is useful, because it lets us pick out the vertex of a parabola really quickly just by looking at the equation.

Complete step by step solution:
In this given problem,
We have a quadratic equation with Vertex- \[(5,5)\] and Point- \[(6,6)\]
For this question the two forms of a parabola's equation should be followed:
Standard form: \[y = a{x^2} + bx + c\]
Vertex form: \[y = a{(x - h)^2} + k\] (with vertex at \[(h,k)\] )
First, we use the values given in question to form vertex equation
 \[ \Rightarrow y = a{(x - 5)^2} + 5\] Taking \[h\] =5 and \[k\] =5 since Vertex is \[(5,5)\] …………..(1)
Now in order to find out \[a\] we use the information given about Point- \[(6,6)\] in above equation
 \[ \Rightarrow 6 = a{(6 - 5)^2} + 5\]
 \[ \Rightarrow 6 = a + 5\]
 \[\therefore a = 1\]
Since we have all the information, we can use the standard form of to form a quadratic equation as follows from the vertex form in (1):
 \[ \Rightarrow y = a{(x - 5)^2} + 5\]
Substituting \[a = 1\] ,
 \[ \Rightarrow y = {(x - 5)^2} + 5\]
Factoring \[{(x - 5)^2}\] with the help of formula:
 \[{(a - b)^2} = {a^2} - 2ab + {b^2}\]
Substituting \[a = x\] and \[b = 5\] we get,
 \[ \Rightarrow y = ({x^2} - 10x + 25) + 5\]
Opening the brackets,
 \[ \Rightarrow y = {x^2} - 10x + 25 + 5\]
 \[\therefore y = {x^2} - 10x + 30\]
Hence, we get the final quadratic equation as: \[y = {x^2} - 10x + 30\].

Note: A parabolic equation resembles a quadratic equation in appearance. You can find the vertex and standard forms of a parabolic equation and write the parabola algebraically with only two of the parabola's points, the vertex and one other.
The vertex \[(5,5)\] of given equation is shown graphically for better understanding:

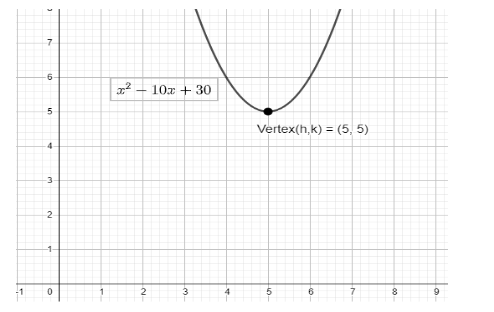
Remember to use the vertex form of equation first and find out the missing data to arrive at the standard equation form.