Question

How much work does it take to push an object with a mass of $ 1kg $ up a $ 6m $ ramp, if the ramp has an incline of $ \dfrac{5\pi }{12} $ and a kinetic friction coefficient of $ 4 $ ?

Answer 1

Hint :In such questions we can just draw a free body diagram and balance the forces. By balancing the forces we can get the actual force required to push the object upwards. Once we get the force required to push the object we can easily find the work done by using its formula which is the dot product of force required times the displacement. In the question we have already given the displacement which is $ 6m $ and we only need to find force.
Work done: $ W=F\cdot d $
Where $ F $ is the force and $ d $ is the displacement.
Frictional force $ f=\mu N $
Where $ \mu $ is the friction coefficient and $ N $ is the normal force.

Complete Step By Step Answer:
Let us first draw the free body diagram for the given situation

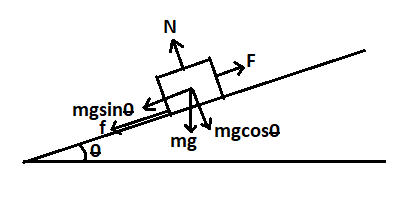
In the above diagram $ F $ is the upward force acting on the object to push upwards, $ f $ is the frictional force which will act opposite to the direction of motion, $ mg $ ( $ m $ is mass of the object and $ g $ is gravitational acceleration) is the downward gravitational pull acting on the object, $ mgcos\theta $ and $ mgsin\theta $ are the cosine and sine components respectively of the $ mg $ whereas $ N $ is the normal force on the object. Here $ \theta $ is the angle which the ramp makes with the horizontal surface and its value according to the question is $ \theta =\dfrac{5\pi }{12} $ .
We know that frictional force is given as the product of coefficient of friction and normal force, so we have
 $ f=\mu N $
where, $ \mu $ is coefficient of friction and according to question, $ \mu =4 $ and from the above diagram we can see that cosine component of $ mg $ balances the normal force, so we can rewrite the above equation as
 $ f=\mu mg\cos \theta $
Similarly, by balancing the forces in the above diagram we get $ F $ as
$F=f+mg\sin \theta $
$ \Rightarrow F=\mu mg\cos \theta +mg\sin \theta $
$\Rightarrow F=mg(\mu \cos \theta +\sin \theta ) $
Substituting the values we get ( $ m=1kg,g=9.8m/s $ )
 $\Rightarrow F=(1)(9.8)\left[ (4)\cos \left( \dfrac{5\pi }{12} \right)+\sin \left( \dfrac{5\pi }{12} \right) \right] $
 $ \Rightarrow F=9.8\left[ 1.03+0.97 \right] $
 $ \Rightarrow F=9.8\times 2=19.6N $
Now, let us calculate the work done. Work done is the force $ F $ required to displace any object ‘ $ d $ ’ meters from its initial position and it is given as dot product of force and displacement, i.e.
 $ W=F\cdot d $
As the force and displacement takes place in the same direction, work done can be just given as force times displacement.
 $ W=Fd $
Substituting value of F calculated above and $ d=6m $ , we have
 $W=19.6\times 6 $
 $W=117.6J $

Note :
In case force and displacement is perpendicular to each other then, no work will be done whereas if they are in opposite directions negative work is done due to the dot product. Also while calculating note that the value of angle is in radian and not in degrees. In case the object was pulled upward with the help of string then we also have to consider the tension.