Question

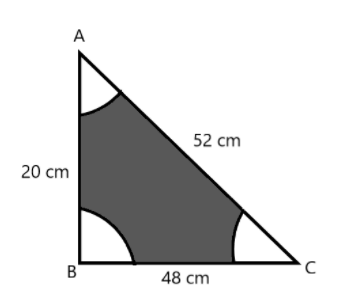
With vertices A, B and C of a triangle ABC as centres, arcs are drawn with radii $ 6{\text{ cm}} $ each (as shown in the figure). If $ AB = 20{\text{ cm}} $ , $ BC = 48{\text{ cm}} $ and $ CA = 52{\text{ cm}} $ , then find the area of the shaded region. (Use $ \pi = 3.14 $ ).

Answer 1

Hint: In order to find the Area of the shaded region, initiate with finding the area of the triangle for that first find what kind of the triangle is given using the sides given. Then find the area of the sectors given. Subtract the area of the three sectors from the area of the triangle, and the obtained area will be the area of the shaded region.
Formula used:
 $ Area = \dfrac{1}{2} \times base \times height $
 $ {\text{Area of sector}} = \dfrac{{\left( {angle} \right)\pi {r^2}}}{{{{360}^ \circ }}} $

Complete step-by-step answer:
Since, we can see from the figure that the main figure is a triangle ABC with sides $ AB = 20{\text{ cm}} $ , $ BC = 48{\text{ cm}} $ and $ CA = 52{\text{ cm}} $ which include three sectors of circle of radius $ 6{\text{ cm}} $ each.
If we subtract the sum of the area of the three sectors from the area of the triangle, we would get the area of the shaded region.
For that we need to find the area of the triangle and the area of the sectors.
Starting with the triangle:
Checking out what kind of triangle is the triangle ABC.
If $ A{B^2} + B{C^2} = A{C^2} $ (Pythagoras Theorem) is satisfied then it’s a right-angled triangle.
In $ A{B^2} + B{C^2} = A{C^2} $ , taking the LHS:
 $ A{B^2} + B{C^2} $
Substituting the values, we get:
 $ \Rightarrow {\left( {20} \right)^2} + {\left( {48} \right)^2} $
 $ \Rightarrow 400 + 2304 $
 $ \Rightarrow 2704 $
Therefore, LHS $ A{B^2} + B{C^2} = 2704 $ ….(1)
In $ A{B^2} + B{C^2} = A{C^2} $ , taking the RHS:
 $ A{C^2} $
Substituting the values, we get:
 $ \Rightarrow {\left( {52} \right)^2} $
 $ \Rightarrow 2704 $
Therefore, RHS $ A{C^2} = 2704 $ ….(2)
Since, from equation 1 and equation 2, we can see that:
LHS=RHS and $ A{B^2} + B{C^2} = A{C^2} $ or Pythagoras Theorem is satisfied then ABC a right-angled triangle.
So, From the area of Right-angled triangle, we get:
 $ Area = \dfrac{1}{2} \times base \times height $
 $ \Rightarrow Area = \dfrac{1}{2} \times BC \times AB $
Substituting the values, we get:
 $ \Rightarrow Area = \dfrac{1}{2} \times 48 \times 20 $
 $ \Rightarrow Area = 24 \times 20 $
 $ \Rightarrow Area = 480 $
Therefore, Area of triangle ABC is $ 480{\text{ c}}{{\text{m}}^2} $ . …….(3)
For the sectors:
Since, we know that the area of sectors $ = \dfrac{{\left( {angle} \right)\pi {r^2}}}{{{{360}^ \circ }}} $ .
Since, all the three sectors have the same radii only at different angles, that is $ \angle A,\angle B,\angle C $ .
So, the area of the three sectors become $ \dfrac{{\left( {\angle A} \right)\pi {{\left( 6 \right)}^2}}}{{{{360}^ \circ }}},\dfrac{{\left( {\angle B} \right)\pi {{\left( 6 \right)}^2}}}{{{{360}^ \circ }}}{\text{ and }}\dfrac{{\left( {\angle C} \right)\pi {{\left( 6 \right)}^2}}}{{{{360}^ \circ }}} $ .
Their sum becomes:
 $ Area = \dfrac{{\left( {\angle A} \right)\pi {{\left( 6 \right)}^2}}}{{{{360}^ \circ }}} + \dfrac{{\left( {\angle B} \right)\pi {{\left( 6 \right)}^2}}}{{{{360}^ \circ }}} + \dfrac{{\left( {\angle C} \right)\pi {{\left( 6 \right)}^2}}}{{{{360}^ \circ }}} $
Taking $ \dfrac{{\pi {{\left( 6 \right)}^2}}}{{{{360}^ \circ }}} $ common, we get:
\[Area = \dfrac{{\pi {{\left( 6 \right)}^2}}}{{{{360}^ \circ }}}\left( {\angle A + \angle B + \angle C} \right)\]
\[ \Rightarrow Area = \dfrac{{3.14 \times 36}}{{{{360}^ \circ }}}\left( {\angle A + \angle B + \angle C} \right)\]
Since, we know that sum of all the interior angles of a triangle is \[{180^ \circ }\], that gives \[\left( {\angle A + \angle B + \angle C} \right) = {180^ \circ }\], substituting it in the above value, we get:
\[ \Rightarrow Area = \dfrac{{3.14 \times 36}}{{{{360}^ \circ }}} \times {180^ \circ }\]
\[ \Rightarrow Area = \dfrac{{3.14 \times 36}}{2}\]
\[ \Rightarrow Area = 3.14 \times 18\]
\[ \Rightarrow Area = 3.14 \times 18\]
\[ \Rightarrow Area = 56.52\]
Therefore, the sum of the area of the three sectors is \[56.52{\text{ c}}{{\text{m}}^2}\]. …….(4)
If we subtract the sum of the area of the three sectors from the area of the triangle, we would get the area of the shaded region.
Subtracting equation (4) from equation (3), we get:
\[ \Rightarrow {\text{Area of the shaded region}} = 480 - 56.52 = 423.48{\text{ c}}{{\text{m}}^2}\]
Therefore, the Area of the shaded region is \[423.48{\text{ c}}{{\text{m}}^2}\].
So, the correct answer is “\[423.48{\text{ c}}{{\text{m}}^2}\]”.

Note: The sum of all the interior angles of a triangle is \[{180^ \circ }\], and this statement is known as the angle sum property of a triangle.
A sector is basically a part of the circle, which includes two radii and one arc between them.
If the triangle was not a right-angled triangle then we would have used Heron’s formula to find the area of the triangle.