Question

Which statement is true about the difference of any two sides of a triangle?
$A.$ It is greater than the third side
$B.$ It is zero
$C.$ It is lesser than the third side
$D.$ It is lesser than zero

Answer 1

Hint: Here we will proceed by constructing a triangle in which we draw a line that intersects the two sides of the triangle such that we get exterior angles $\angle 1$, $\angle 2$,$\angle 3$,$\angle 4$. Then we will use the property that the side opposite to the exterior angle is the longest side. Thus we will get the desired result.

Complete step-by-step answer:
Properties of triangle are-
$ \Rightarrow $ Sum of angles of a triangle is always${180^ \circ }$.
$ \Rightarrow $The exterior angles of a triangle always add up to ${360^ \circ }$.
$ \Rightarrow $The sum of the lengths of any two sides of a triangle is greater than the length of the third side.
$ \Rightarrow $The shortest side is always opposite to the smallest exterior angle. Similarly, the longest side is always opposite to the largest exterior angle.
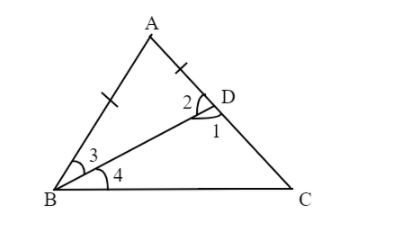
Here in triangle ABC, we will construct a line from point B to opposite side AC which cuts AC into two parts – AD and BD.
Now this construction shows that AB = AD
$ \Rightarrow $In $\vartriangle ABD$ ,
$ \Rightarrow $ $\angle 1$(exterior angle)
$ \Rightarrow $ $\angle 1$>$\angle 3$ (using exterior angle property)
$ \Rightarrow $ Similarly, In $\vartriangle BDC$
$ \Rightarrow $ $\angle 2$ > $\angle 4$ ( using exterior angle property)
$ \Rightarrow $ Also we know that the side opposite to the greater angle is always greater.
$ \Rightarrow $So, In $\vartriangle BDC$
BC is the greater side.
$ \Rightarrow $Similarly, we get BC > CD
$ \Rightarrow $ BC > (AC – AD)
$ \Rightarrow $ AB = AD (Through construction)
$ \Rightarrow $ BC > (AC – AB)
$\therefore $ We conclude that AC and AB are two sides whose difference is smaller than the third side BC.
$ \Rightarrow $Option C is correct.

Note: Here one can get confused between whether to use exterior angle property or interior angle property to solve this type of question because the side opposite to greatest exterior angle is greatest.