Question

Which statement is correct for the given circuit?

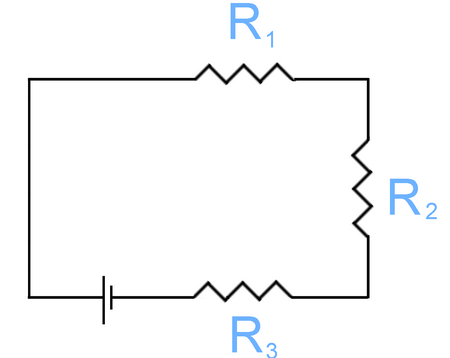
A. \[I\] through \[{R_1} > I\] through \[{R_2}\]
B. \[I\] through \[{R_3} > I\] through \[{R_2}\] and \[{R_1}\]
C. \[I\] through \[{R_2} > I\] through \[{R_3}\] and \[{R_1}\]
D. \[I\] is same in \[{R_1}\], \[{R_2}\] and \[{R_3}\]

Answer 1

Hint – You can start by describing the basic concept of flow of current (concept of movement of electrons), then using the equation \[I = \dfrac{Q}{t}\] as a basis to find out the current flowing through each of the resistors (not mathematically but theoretically) and compare them to reach the solution.

Complete step-by-step answer:
Before moving on to the actual solution, it is very important to understand the basic concept of current. When we say a current is flowing through a material, it is mostly the positive and negatively charged particles that are moving to the end with the opposite charge (due to the electrostatic force of attraction). In the case of electrolysis current flows because of the movement of positive and negative ions. But in the case of the circuit given in the problem, it can be safely assumed that the wires would be made of metals. In case of a metal when a potential difference occurs in between the ends of the circuit, a current starts to flow through the circuit. The current in the case of metal is only due to the movement of the free electrons to the end with positive potential difference. Protons are usually not involved in the flow of current as they are tightly bound to the nucleus.
The formula for current is
\[I = \dfrac{Q}{t}\]
Here
\[I = \]Current,
\[Q = \]Total charge,
\[t = \]Time.
So we now know that the current flowing in a circuit is due to the flow of free electrons. In the given problem the circuit has three resistors \[{R_1}\], \[{R_2}\] and \[{R_3}\]. So the electrons have only one point of entry and one point of exit, so all the electrons would have to go through all the resistors in the same time frame before exiting the circuiting and as \[I = \dfrac{Q}{t}\], so the current in the all resistors will be the same i.e. \[I\] is the same in \[{R_1}\], \[{R_2}\] and \[{R_3}\].
Hence, option D is the correct choice.

Note – The circuit given in the problem has resistors in series combination. Let’s look at what would have happened if the resistors were in a parallel combination. In this case the electrons flowing through the parallel combination would split between the resistors. So as \[I = \dfrac{Q}{t}\], the current flowing through the resistors would be different.