
Which point is considered as the orthocenter of the triangle.
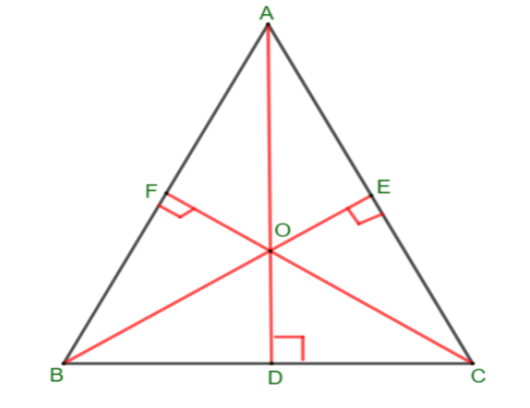

Answer
515.1k+ views
Hint: Here we have to tell which point is called the orthocentre of the triangle. In a question they have given a diagram where we have three perpendicular lines from each of the points. So by considering this diagram and the properties of the orthocentre of the triangle we are going to determine which point is called the orthocentre of the triangle.
Complete step by step solution:
The orthocenter of a triangle is the point where the perpendicular drawn from the vertices to the opposite sides of the triangle intersect each other.
The properties of orthocenter of a triangle is given by:
I.For an acute angle triangle, the orthocenter lies inside the triangle.
II.For the obtuse angle triangle, the orthocenter lies outside the triangle.
III.For a right triangle, the orthocenter lies on the vertex of the right angle.
Now consider the triangle which is given in the question. The given triangle is an acute angle triangle where all the angles of a triangle are less than a \[{90^ \circ }\].
There is a line from a point A which is perpendicular to the line BC. The line from a point B which is perpendicular to AC. The line from a point C which is perpendicular to the line AB. These three perpendicular lines meet at a common point and it is named as O. From the definition of the orthocenter of a triangle. The point O is the orthocenter of a triangle.
So, the correct answer is “ Point O”.
Note: There is no direct formula to calculate the orthocenter of the triangle. It lies inside for an acute and outside for an obtuse triangle. So when the points of triangle is given we have to determine the slope of the line, that is given by Slope of a line = \[\dfrac{{{y_2} - {y_1}}}{{{x_2} - {x_1}}}\] and perpendicular slope = \[\dfrac{1}{{Slope\,of\,line}}\], Then \[y - {y_1} = m(x - {x_1})\] using this we can determine equation of altitude of respective coordinates. we can determine the orthocenter value.
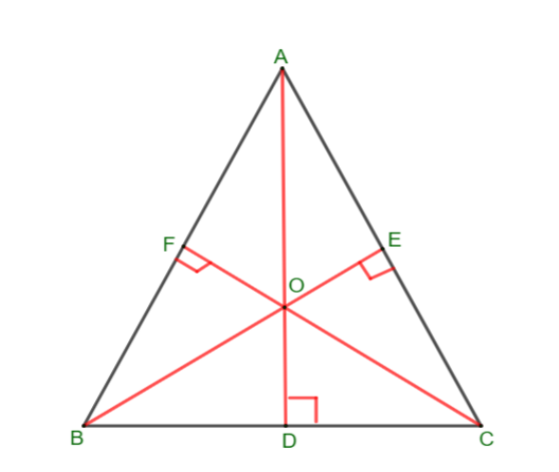
Complete step by step solution:
The orthocenter of a triangle is the point where the perpendicular drawn from the vertices to the opposite sides of the triangle intersect each other.
The properties of orthocenter of a triangle is given by:
I.For an acute angle triangle, the orthocenter lies inside the triangle.
II.For the obtuse angle triangle, the orthocenter lies outside the triangle.
III.For a right triangle, the orthocenter lies on the vertex of the right angle.
Now consider the triangle which is given in the question. The given triangle is an acute angle triangle where all the angles of a triangle are less than a \[{90^ \circ }\].

There is a line from a point A which is perpendicular to the line BC. The line from a point B which is perpendicular to AC. The line from a point C which is perpendicular to the line AB. These three perpendicular lines meet at a common point and it is named as O. From the definition of the orthocenter of a triangle. The point O is the orthocenter of a triangle.
So, the correct answer is “ Point O”.
Note: There is no direct formula to calculate the orthocenter of the triangle. It lies inside for an acute and outside for an obtuse triangle. So when the points of triangle is given we have to determine the slope of the line, that is given by Slope of a line = \[\dfrac{{{y_2} - {y_1}}}{{{x_2} - {x_1}}}\] and perpendicular slope = \[\dfrac{1}{{Slope\,of\,line}}\], Then \[y - {y_1} = m(x - {x_1})\] using this we can determine equation of altitude of respective coordinates. we can determine the orthocenter value.
Recently Updated Pages
Master Class 8 Social Science: Engaging Questions & Answers for Success

Master Class 8 English: Engaging Questions & Answers for Success

Class 8 Question and Answer - Your Ultimate Solutions Guide

Master Class 8 Maths: Engaging Questions & Answers for Success

Master Class 8 Science: Engaging Questions & Answers for Success

Master Class 7 English: Engaging Questions & Answers for Success

Trending doubts
What is BLO What is the full form of BLO class 8 social science CBSE

Citizens of India can vote at the age of A 18 years class 8 social science CBSE

Full form of STD, ISD and PCO

Advantages and disadvantages of science

Right to vote is a AFundamental Right BFundamental class 8 social science CBSE

What are the 12 elements of nature class 8 chemistry CBSE





