Question

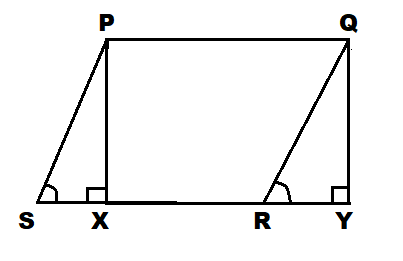
Which option is equal to PX in the given figure?

A) QY
B) 2QY
C) \[\dfrac{1}{2}QY\]
D) XR

Answer 1

Hint:
We will use the properties of a parallelogram. And then we will use that \[\angle PSX\] and \[\angle QRY\] are equal. And then we will use Pythagoras theorem and show that PX is equal to QY.

Complete step by step solution:
PQRS is a parallelogram. And \[\angle PXS\] and \[\angle QYR\] are right angled triangles.
Since, PQRS is a parallelogram
In a parallelogram, opposite sides are equal.
Therefore, PS = QR … (1)
Let \[\angle PSX\] and \[\angle QRY\] measure \[\theta \].
Using Pythagoras theorem in triangle PXS.
Using, \[\sin \theta = \dfrac{{opp.}}{{hyp.}}\] , so we have
\[ \Rightarrow \sin \theta = \dfrac{{PX}}{{PS}}\] … (2)
On cross multiplication we get,
\[ \Rightarrow PX = PS\sin \theta \] … (3)
Using Pythagoras theorem in triangle QRY
Using, \[\sin \theta = \dfrac{{opp.}}{{hyp.}}\], so we have
\[ \Rightarrow \sin \theta = \dfrac{{QY}}{{QR}}\] … (4)
On cross multiplication, we get
\[ \Rightarrow QY = QR\sin \theta \] … (5)
From equation (1) and (5), we have
\[ \Rightarrow QY = PS\sin \theta \] … (6)
From equation (3) and (6), we get
\[ \Rightarrow PX = QY\]
Hence, PX = QY

Therefore, option (A) is the correct option.

Note:
Some properties of parallelogram are:
1) In a parallelogram, opposite sides are equal.
2) If in a quadrilateral, each pair of opposite angles is equal, then it is a parallelogram.
3) A quadrilateral is a parallelogram if a pair of opposite sides are equal and parallel.
4) The diagonals of parallelograms bisect each other.