Question

Which one of the following is not a Pythagorean triples?
A. $11,60,61$
B. $16,63,65$
C. $28,45,53$
D. $30,80,99$

Answer 1

Hint: Here we have been given four options and we have to find which of them is not a Pythagorean triple. Firstly we will write the rule which should be satisfied in order to be a Pythagorean triples which is ${{a}^{2}}+{{b}^{2}}={{c}^{2}}$ .Then we will check this condition for each options by putting the biggest number on the right side of the formula and the other two numbers on the left side. Finally if both side values are equal it is a Pythagorean triple and we get our desired answer.

Complete step-by-step answer:
For finding which of the options is not Pythagorean triple we will use Pythagorean Theorem. It states that if we have been given $\Delta ABC$ shown below:

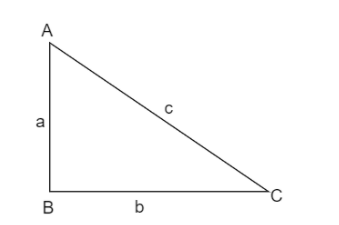
Then
${{a}^{2}}+{{b}^{2}}={{c}^{2}}$….$\left( 1 \right)$
Where, $aSubstitute the numbers from each option in the above formula by taking the biggest number on the right side.
A. $11,60,61$
Substituting $a=11,b=60$ and $c=61$ in equation (1)
$\Rightarrow {{11}^{2}}+{{60}^{2}}={{61}^{2}}$
$\Rightarrow 121+3600=3721$
On simplifying we get,
$\Rightarrow 3721=3721$
As both side values are the same it is a Pythagorean triple. It can be drawn as:

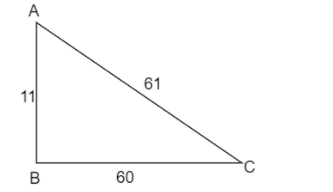
B. $16,63,65$
Substituting $a=16,b=63$ and $c=65$ in equation (1)
$\Rightarrow {{16}^{2}}+{{63}^{2}}={{65}^{2}}$
$\Rightarrow 256+3969=4225$
On simplifying we get,
$\Rightarrow 4225=4225$
As both side values are the same it is a Pythagorean triple. It can be drawn as:

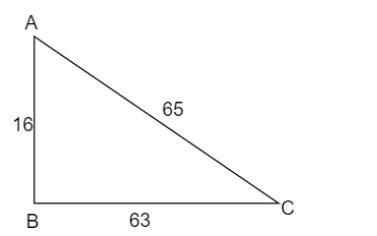
C. $28,45,53$
Substituting $a=28,b=45$ and $c=53$ in equation (1)
$\Rightarrow {{28}^{2}}+{{45}^{2}}={{53}^{2}}$
$\Rightarrow 784+2025=2809$
On simplifying we get,
$\Rightarrow 2809=2809$
As both side values are the same it is a Pythagorean triple. It can be drawn as:

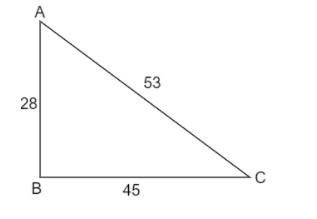
D. $30,80,99$
Substituting $a=30,b=80$ and $c=99$ in equation (1)
$\Rightarrow {{30}^{2}}+{{80}^{2}}={{99}^{2}}$
$\Rightarrow 900+6400=9801$
On simplifying we get,
$\Rightarrow 7300=9801$
As both side values are not the same it is not a Pythagorean triple. The triangle can’t be drawn.
So, the correct answer is “Option D”.

Note: Pythagorean triples are those integers which satisfy Pythagoras Theorem. Pythagoras theorem states that the sum of the square of base and height of a right-angle triangle is equal to the square of its hypotenuse. Hypotenuse is the longest side of the triangle and that is the reason we have taken the biggest value in each case on the right side of the formula.