Question

Which of the following vectors best represents the vector \[A + B\]?

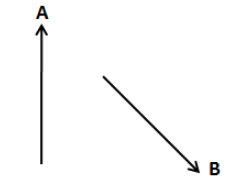
A.

B.

C.

D.

Answer 1

Hint: Recall the triangle law of vector addition. Use the tip-to-tail method to move the vector B to join it with vector A. From the triangle law of vector addition, determine the resultant of the two vectors A and B.

Complete answer:
We have given the two vectors and we are asked to determine the vector sum of the two vectors. To do so, we have to use the law of vector addition. Thus, let’s recall the law of vector addition.
We have two laws of vector addition: triangle law of vector addition and parallelogram law of vector addition. According to triangle law of vector addition, if the two vectors are given such that they represent the two sides of the triangle, then the third side of the triangle is the resultant of the two vectors. If we have two vectors \[\vec A\] and \[\vec B\], and these vectors represents the two sides of the triangle as shown in the figure below,

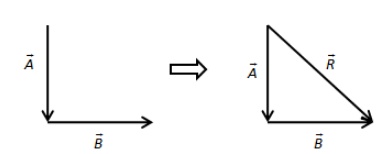
We have to add two given vectors using tip-to-tail method which states that to move two vectors for addition, the tail of the second vector B should lie on the tip of the first vector A. Therefore, joining these two vectors, we get,

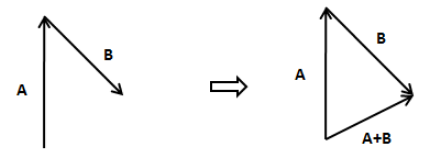
Thus, from the given options, the option (A) best represents the resultant vector \[A + B\] of the two vectors A and B.

So, the correct answer is option A.

Note:To use triangle law of vector addition, the two vectors must represent the two sides of the triangle. If the two vectors have opposite directions, the resultant of these vectors is the vector sum. That is if one of the vector A is along the positive x-direction and other vector B is along negative x-axis, then the resultant is \[\vec A + \left( { - \vec B} \right) = \vec A - \vec B\].