Question

Which of the following statements are correct and which are incorrect. State reasons for your answer.
[1] The opposite sides of a quadrilateral are parallel.
[2] If one angle of a quadrilateral is $60{}^\circ $ then the other angles are $120{}^\circ ,60{}^\circ ,120{}^\circ $

Answer 1

Hint: Recall the definition of a parallelogram and a quadrilateral. Using the definition and the properties of a parallelogram and a quadrilateral verify which of the statements is correct. Use the fact that the sum of angles in a quadrilateral should be $360{}^\circ $ and as long as this constraint is maintained, the angles can be anything. Use the fact that a kite and a trapezium are also quadrilaterals. If the statement is correct, prove the statement and if the statement is incorrect, give a counter-example.

Complete step-by-step solution -
Before solving the question, we need to understand the definitions and properties of a parallelogram and a quadrilateral.
Quadrilateral: A quadrilateral is a closed figure consisting of four sides. The sum of the angles of a quadrilateral is 360(degrees). A quadrilateral is not completely determined by one of its angles.
Parallelogram: A quadrilateral in which the opposite pair of sides are parallel is known as a parallelogram. In a parallelogram, opposite sides are equal and parallel to each other.
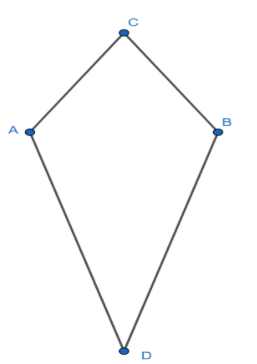
Statement I is incorrect since it is not necessary that the opposite sides of a quadrilateral are parallel. The quadrilateral in which the opposite sides are parallel is a parallelogram. An example of a quadrilateral in which the opposite sides are not parallel is kite as shown below

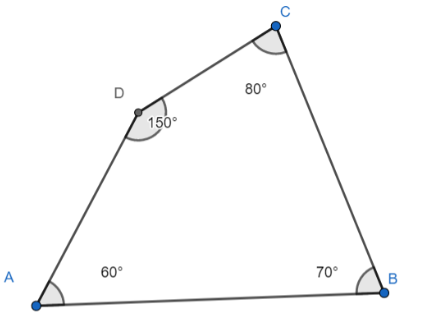
Statement II is incorrect since there exists a quadrilateral with angles as $60{}^\circ ,70{}^\circ ,80{}^\circ ,150{}^\circ $ , as shown below

Note: The most likely mistake that a student can make in this question is that he checks that the angle sum property in statement II is satisfied and hence the statement is correct. It, however, should be noted that the statement is conditional, and the implication part is not correct due to the existence of quadrilaterals which do not follow the implied part as shown in the above solution.