Question

Which of the following statements about the function \[y = f\left( x \right)\] graphed here are true,

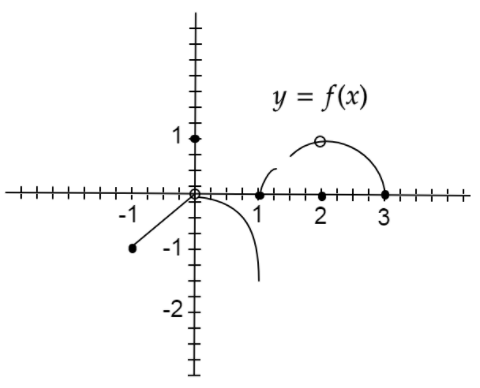
A. \[{\lim _{x \to 2}}f\left( x \right)\] does not exist
B. \[{\lim _{x \to 2}}f\left( x \right) = 1\]
C. \[{\lim _{x \to 1}}f\left( x \right)\] does not exist
D. \[{\lim _{x \to {x_0}}}f\left( x \right)\] exists at every point \[{x_0}\] in \[\left( { - 1,1} \right)\]

Answer 1

Hint:In the above given question, we are given a graph of the function \[y = f\left( x \right)\] . As we can see, the graph of the function is not continuous everywhere, i.e. the graphs is broken at few intervals and points. That means the graph is discontinuous at those points. In other words, the limit of the function \[y = f\left( x \right)\] does not exist at those broken intervals or points. We have to determine which one of the four given options is correct.

Complete step by step answer:
We are given the graph of the function \[y = f\left( x \right)\]. We have to determine if the limit of the given function exists or not for four given options.In order to approach the solution, we need to use the formula of right and left hand limit of a function at a point, that is given as: if,
\[ \Rightarrow {\lim _{x \to {a^ - }}}f\left( x \right) = i{m_{x \to {a^ + }}}f\left( x \right) = f\left( a \right)\]
Then, the limit of the function \[f\left( x \right)\] exists at the point \[a\] .

Now we will check each option one by one.
A. \[{\lim _{x \to 2}}f\left( x \right)\] does not exist
Here,
\[ \Rightarrow {\lim _{x \to {2^ - }}}f\left( x \right) = {\lim _{x \to {2^ + }}}f\left( x \right) = 1 \ne f\left( 2 \right) = 0\]
Hence, \[{\lim _{x \to 2}}f\left( x \right)\] does not exist.

B. \[{\lim _{x \to 2}}f\left( x \right) = 1\]
Here, from the above case we have
\[ \Rightarrow {\lim _{x \to {2^ - }}}f\left( x \right) = {\lim _{x \to {2^ + }}}f\left( x \right) = 1 \ne f\left( 2 \right) = 0\]
Therefore, \[{\lim _{x \to 2}}f\left( x \right) \ne 1\] .

C. \[{\lim _{x \to 1}}f\left( x \right)\] does not exist
Here, from the graph of the function \[y = f\left( x \right)\] , we have
\[ \Rightarrow {\lim _{x \to {1^ - }}}f\left( x \right) \ne {\lim _{x \to {1^ + }}}f\left( x \right) = f\left( 1 \right) = 1\]
Hence, \[{\lim _{x \to 1}}f\left( x \right)\] does not exist.

D. \[{\lim _{x \to {x_0}}}f\left( x \right)\] exists at every point \[{x_0}\] in \[\left( { - 1,1} \right)\]
From the graph we have the limit at \[0 \in \left( { - 1,1} \right)\] as,
\[ \Rightarrow {\lim _{x \to {0^ - }}}f\left( x \right) = {\lim _{x \to {0^ + }}}f\left( x \right) = 0 \ne f\left( 0 \right) = 1\]
Hence, the \[{\lim _{x \to {x_0}}}f\left( x \right)\] does not exists at every point \[{x_0}\] in \[\left( { - 1,1} \right)\].

Therefore, the correct options are only A and C.

Note:Continuous functions are functions that have no restrictions throughout their domain or a given interval. Their graphs won't contain any asymptotes or signs of discontinuities as well. A function which is continuous on an interval does not always mean that the function is as well as differentiable. Whereas if a function is differentiable on an interval then it is also a continuous function on the given interval.