Question

Which of the following points lies in the second quadrant?
$A). (x, -y)$
$B). (-x, -y)$
$C). (-x, y)$
$D). (x, y)$

Answer 1

Hint: First we have to define what the terms we need to solve the problem are.
First of all, there are some axes which are the directions of the two-dimensional cartesian system or Cartesian means pair of elements that will divide the plane of two dimensions into four separate different types of region. And that four different separated regions are called the quadrant of the two-dimensional Cartesian system.

Complete step-by-step solution:
Since that plane is divided by a two-dimensional system it will divide four of equal parts, the quadrants are first quadrant which is in the right hand of the two-dimensional, since as follows by second quadrant, third quadrant and finally the fourth quadrant. And these equal quadrants are represented as the axes with $x - axis$ and $y - axis$ and they will contain different values and alternatives of positive and negative signs.

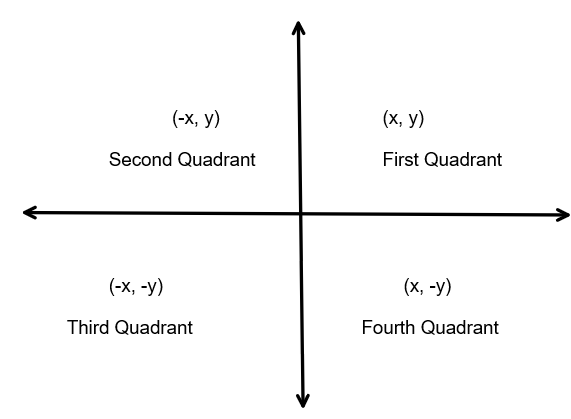
Since as you see in the right-hand side top is the first quadrant and it will consist of positive x and positive y axes, so the x and y both are positives in the $1^{st}$ quadrant. And the angle of the first quadrant is zero to ninety degree. Since as you see in the right-hand side below is the fourth quadrant and it will consist of positive x and negative y axes, so that it will be the fourth in the quadrant. And the angle of the fourth quadrant is two seventy to three sixty degrees. Also, the third quadrant contains both negatives which is the inverse of the first quadrant.
Hence as you see in the left-hand side top is the second quadrant and it will consist of negative x and positive y axes, so that it will be the second in the quadrant. And the angle of the second quadrant is ninety to one eighty degree.
Therefore: in the second quadrant we clearly see that $C)( - x,y)$ is the lying point, and as all other options will be eliminated as per angles of quadrant and per positive, negative signs

Note: As we see this quadrant is the angle of anti-clock wise direction rounding, if it is in the clockwise the answers maybe suffer but that will not be going to happen, as per the degrees of the quadrant in zero, ninety, one eighty, two seventy.