Question

Which of the following options is/are true for wheel of Theodorus?
$\begin{align}
  & \text{a) It doesn }\!\!'\!\!\text{ t have any isosceles triangle}\text{.} \\
 & \text{b) The spiral chord is strated with an isosceles triangle with each leg having length 2 units}\text{.} \\
 & \text{c) The spiral is stated with an isosceles right angle triangle each having unit length}\text{.} \\
 & \text{d)None of these}\text{.} \\
\end{align}$

Answer 1

Hint:Now to construct the wheel of Theodorus we start with a triangle such that two of its side are of length 1 unit and perpendicular to each other. Now we draw the third side. Now we will again take a unit length perpendicular to this side and form another triangle. We will go on with this process to form a wheel. Now to find the length of the third side in each step we will use the Pythagoras theorem.

Complete step by step answer:
Now let us first understand the wheel of Theodorus.
$\Rightarrow$ Now to construct this we will first start with two sides, both length 1 unit perpendicular to each other.

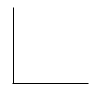
$\Rightarrow$ Now connect the endpoints to form a triangle.

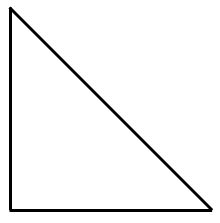
$\Rightarrow$ Now we know that the sides are of length 1 unit.
$\Rightarrow$ Hence by Pythagoras theorem we have length of hypotenuse is $\sqrt{{{1}^{2}}+{{1}^{2}}}=\sqrt{2}$
Now again draw a unit side perpendicular to one end of the hypotenuse. Hence we get

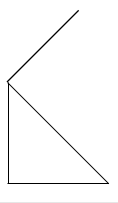
$\Rightarrow$ Now again join the two sides to form a triangle.

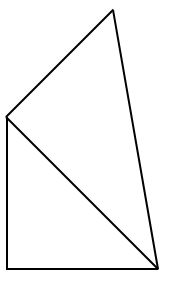
$\Rightarrow$ Now in this new triangle, we have one length is $\sqrt{2}$ and another is 1.
Hence we get the length of hypotenuse is $\sqrt{{{\left( \sqrt{2} \right)}^{2}}+{{1}^{2}}}=\sqrt{2+1}=\sqrt{3}$
$\Rightarrow$ Now we continue these steps after 5 triangles we get a structure in the form of

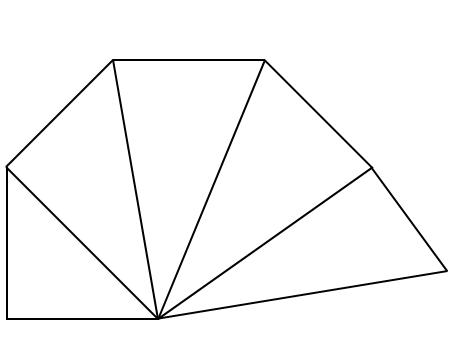
Now as we keep continuing this we can see the structure forming a wheel.
$\Rightarrow$ This is called the wheel of Theodore.
Now consider the given options
Now in the first step since both, the sides of the triangle are of length 1 unit the first triangle is an isosceles triangle. Hence option a is false.
Now from step 2 onwards, we can see that the triangles are not an isosceles triangle. Hence option b is also false.
$\Rightarrow$ Now as we discussed the triangles in the first step are an isosceles triangle of unit length. Hence option c is the correct option.

Note: Note that here in each step one side of the triangle is always 1 and the other side of the triangle is changing. For ${{n}^{th}}$ step we will have one side as $\sqrt{n}$ and other side as 1 and hence the hypotenuse in ${{n}^{th}}$ triangle will be $\left( \sqrt{n+1} \right)$ hence at any given point we have length of sides of triangle.