Question

Which of the following options is correct according to the principle of moments.
A. Product of anticlockwise force = Product of clockwise force
B. Sum of anticlockwise force = Sum of clockwise force
C. Both
D. None

Answer 1

Hint: To solve this question we must have a basic understanding of what is moment.
Moment: The turning effect produced by a force is termed as the moment. It is the product of the magnitude of force multiplied by the perpendicular distance from the line of action of the force to the pivot or the point where the object will turn.

Complete step by step answer:
Principle of moments : The principle of moments states that when a body is in rotational equilibrium, then the total sum of the anticlockwise moment is equal to the total sum of the clockwise moment.
In equilibrium:
The total sum of anticlockwise moment = Total sum of clockwise moment
So, none of the options are correct.
This principle can be explained by considering two people balanced on a seesaw.

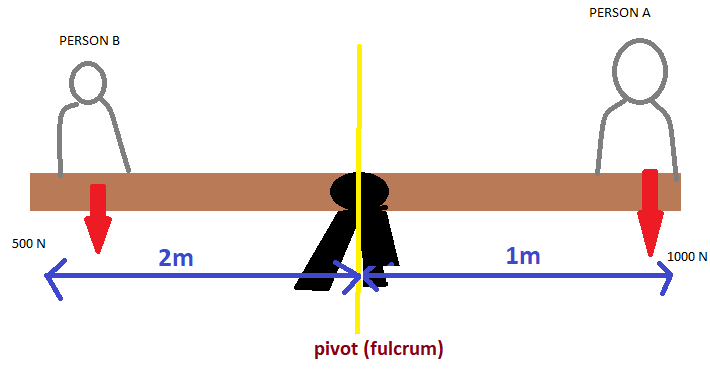
Here, both the persons exert a downward force on the seesaw due to their weights.
Person A’s weight is trying to turn the seesaw in an anticlockwise direction while the person B’s weight is trying to turn the seesaw in a clockwise direction.
In balanced condition:
Moment due to Person A = Force x perpendicular distance from fulcrum
$ = 1000 \times 1 = 1000{\text{ N - m}}$
Moment due Person B = Force x perpendicular distance from fulcrum
\[ = 500\; \times 2\;\; = {\text{ }}1000{\text{ N - m}}\]
Moment due to Person A = Moment due Person B
$ \Rightarrow $Anticlockwise moment = Clockwise moment
Therefore, seesaw is in equilibrium.

So, the correct answer is “Option B”.

Note:
Usually, the sign convention for the moment of force is taken as follows:
Clockwise moment $ \Rightarrow $ positive sign.
Anticlockwise moment $ \Rightarrow $ negative sign.
Moment of force (Newton-meter) = force (Newton) $ \times $ perpendicular distance from the force to the pivot (meter).