
Which of the following is/are positive?
A. ${\log _{\sin 1}}\tan 1$
B. ${\log _{\cos 1}}\left( {1 + \tan 3} \right)$
C. ${\log _{{{\log }_{10}}5}}\left( {\cos \theta + \sec \theta } \right)$
D. ${\log _{\tan {{15}^o}}}\left( {2\sin {{18}^o}} \right)$
Answer
478.5k+ views
Hint: In this question, from the given functions, we have to tell the positive ones. We have that, in ${\log _a}x$ , if $a > 1$ and $x > 1$ or $a < 1$ and $x < 1$ then, ${\log _a}x > 0$ , otherwise, it is negative.
$\tan \theta $ is always an increasing function, whereas, $\sin \theta $ and $\cos \theta $ are neither increasing nor decreasing.
Complete answer:
Given are four logarithmic functions.
To tell which of these are positive.
Firstly, we know, the graph of ${\log _a}x$ , when $a > 1$ is given by
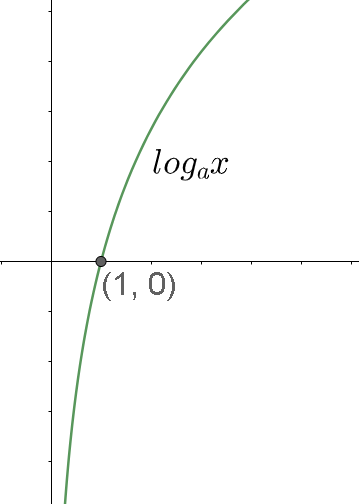
Then, ${\log _a}x > 0$ , when $x > 1$ .
And when $a < 1$ , the graph is given by
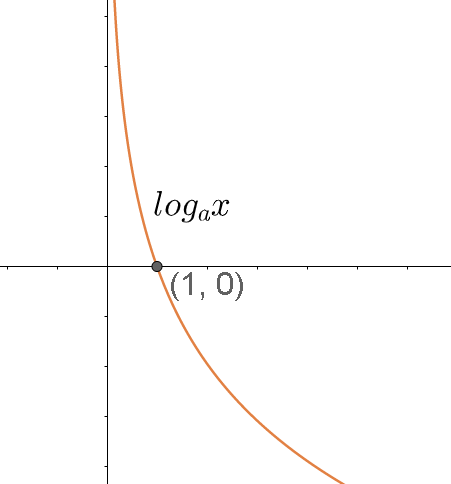
Then, ${\log _a}x > 0$ , when $x < 1$ .
Now, consider the function, ${\log _{\sin 1}}\tan 1$ , we have, $\dfrac{\pi }{2} = \dfrac{{3.14}}{2} > 1$ , so, $\sin \dfrac{\pi }{2} > \sin 1$ which gives $\sin 1 < 1$ .
And, $\dfrac{\pi }{4} = \dfrac{{3.14}}{4} < 1$ , so, $\tan \dfrac{\pi }{4} < \tan 1$ which give $\tan 1 > 1$ . Now, $\sin 1 < 1$ and $\tan 1 > 1$ , hence, ${\log _{\sin 1}}\tan 1 < 0$ .
Now, consider the function, ${\log _{\cos 1}}\left( {1 + \tan 3} \right)$ , $0 < 1 < \dfrac{\pi }{2}$ , so, $\cos 0 > \cos 1 > \cos \dfrac{\pi }{2}$ , since, the function is decreasing for $0 < \theta < \pi $ , hence, $\cos 1 < 1$
And, $\dfrac{\pi }{2} < 3 < \pi $ , which means it is in the second quadrant, and the second quadrant $\tan $ is negative, which means $1 + \tan 3 < 1$ .
Now, $\cos 1 < 1$ and $1 + \tan 3 < 1$ , hence, ${\log _{\cos 1}}\left( {1 + \tan 3} \right) > 0$ .
Now, consider the function, ${\log _{\tan {{15}^o}}}\left( {2\sin {{18}^o}} \right)$ , we know, $\sin {18^o} < \sin {30^o}$ , which means, $\sin {18^o} < \dfrac{1}{2}$ i.e., $2\sin {18^o} < 1$ .
And, we know, $\tan {15^o} < \tan {45^o}$ , which gives, $\tan {15^o} < 1$ . Now, $2\sin {18^o} < 1$ and $\tan {15^o} < 1$ , so, ${\log _{\tan {{15}^o}}}\left( {2\sin {{18}^o}} \right) > 0$ .
Now, at last, consider the function, ${\log _{{{\log }_{10}}5}}\left( {\cos \theta + \sec \theta } \right)$ , we know, ${\log _{10}}5 < {\log _{10}}10$ i.e., ${\log _{10}}5 < 1$ .
And, we know, the Arithmetic mean is always greater than the geometric mean, therefore, $\dfrac{{\left( {\cos \theta + \sec \theta } \right)}}{2} > {\left( {\cos \theta \cdot \sec \theta } \right)^{\dfrac{1}{2}}}$ , which gives, $\cos \theta + \sec \theta > 2 > 1$ .
Now, ${\log _{10}}5 < 1$ and $\cos \theta + \sec \theta > 2 > 1$ , hence, ${\log _{{{\log }_{10}}5}}\left( {\cos \theta + \sec \theta } \right) < 0$ .
Thus, ${\log _{\tan {{15}^o}}}\left( {2\sin {{18}^o}} \right)$ and ${\log _{\cos 1}}\left( {1 + \tan 3} \right)$ are positive.
Therefore, the correct option is B and C
Note: We know that, $\sec \theta $ is reciprocal of $\cos \theta $ .
“Arithmetic mean is always greater than the geometric mean” is true for every function or equation.
For checking, if a logarithmic function is positive or negative, we have to check if $a$ and $x$ are greater than or less than $1$ , if the sign of $a$ and $x$ are same i.e., either both greater than $1$ or both less than $1$, then, the logarithmic function is positive, and if the sign of $a$ and $x$ are not same, i.e., one is greater than $1$ and other is less than $1$, then the logarithmic function is negative.
$\tan \theta $ is always an increasing function, whereas, $\sin \theta $ and $\cos \theta $ are neither increasing nor decreasing.
Complete answer:
Given are four logarithmic functions.
To tell which of these are positive.
Firstly, we know, the graph of ${\log _a}x$ , when $a > 1$ is given by
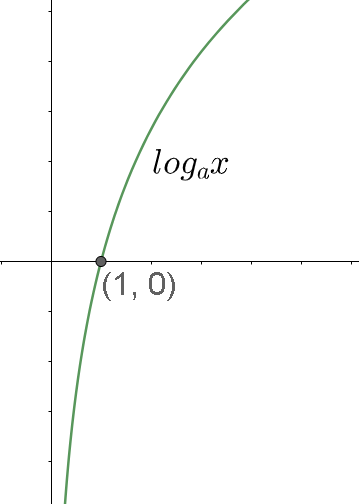
Then, ${\log _a}x > 0$ , when $x > 1$ .
And when $a < 1$ , the graph is given by
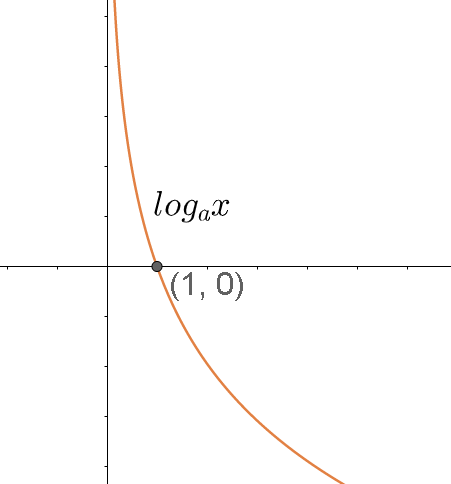
Then, ${\log _a}x > 0$ , when $x < 1$ .
Now, consider the function, ${\log _{\sin 1}}\tan 1$ , we have, $\dfrac{\pi }{2} = \dfrac{{3.14}}{2} > 1$ , so, $\sin \dfrac{\pi }{2} > \sin 1$ which gives $\sin 1 < 1$ .
And, $\dfrac{\pi }{4} = \dfrac{{3.14}}{4} < 1$ , so, $\tan \dfrac{\pi }{4} < \tan 1$ which give $\tan 1 > 1$ . Now, $\sin 1 < 1$ and $\tan 1 > 1$ , hence, ${\log _{\sin 1}}\tan 1 < 0$ .
Now, consider the function, ${\log _{\cos 1}}\left( {1 + \tan 3} \right)$ , $0 < 1 < \dfrac{\pi }{2}$ , so, $\cos 0 > \cos 1 > \cos \dfrac{\pi }{2}$ , since, the function is decreasing for $0 < \theta < \pi $ , hence, $\cos 1 < 1$
And, $\dfrac{\pi }{2} < 3 < \pi $ , which means it is in the second quadrant, and the second quadrant $\tan $ is negative, which means $1 + \tan 3 < 1$ .
Now, $\cos 1 < 1$ and $1 + \tan 3 < 1$ , hence, ${\log _{\cos 1}}\left( {1 + \tan 3} \right) > 0$ .
Now, consider the function, ${\log _{\tan {{15}^o}}}\left( {2\sin {{18}^o}} \right)$ , we know, $\sin {18^o} < \sin {30^o}$ , which means, $\sin {18^o} < \dfrac{1}{2}$ i.e., $2\sin {18^o} < 1$ .
And, we know, $\tan {15^o} < \tan {45^o}$ , which gives, $\tan {15^o} < 1$ . Now, $2\sin {18^o} < 1$ and $\tan {15^o} < 1$ , so, ${\log _{\tan {{15}^o}}}\left( {2\sin {{18}^o}} \right) > 0$ .
Now, at last, consider the function, ${\log _{{{\log }_{10}}5}}\left( {\cos \theta + \sec \theta } \right)$ , we know, ${\log _{10}}5 < {\log _{10}}10$ i.e., ${\log _{10}}5 < 1$ .
And, we know, the Arithmetic mean is always greater than the geometric mean, therefore, $\dfrac{{\left( {\cos \theta + \sec \theta } \right)}}{2} > {\left( {\cos \theta \cdot \sec \theta } \right)^{\dfrac{1}{2}}}$ , which gives, $\cos \theta + \sec \theta > 2 > 1$ .
Now, ${\log _{10}}5 < 1$ and $\cos \theta + \sec \theta > 2 > 1$ , hence, ${\log _{{{\log }_{10}}5}}\left( {\cos \theta + \sec \theta } \right) < 0$ .
Thus, ${\log _{\tan {{15}^o}}}\left( {2\sin {{18}^o}} \right)$ and ${\log _{\cos 1}}\left( {1 + \tan 3} \right)$ are positive.
Therefore, the correct option is B and C
Note: We know that, $\sec \theta $ is reciprocal of $\cos \theta $ .
“Arithmetic mean is always greater than the geometric mean” is true for every function or equation.
For checking, if a logarithmic function is positive or negative, we have to check if $a$ and $x$ are greater than or less than $1$ , if the sign of $a$ and $x$ are same i.e., either both greater than $1$ or both less than $1$, then, the logarithmic function is positive, and if the sign of $a$ and $x$ are not same, i.e., one is greater than $1$ and other is less than $1$, then the logarithmic function is negative.
Recently Updated Pages
Master Class 10 Computer Science: Engaging Questions & Answers for Success

Master Class 10 General Knowledge: Engaging Questions & Answers for Success

Master Class 10 English: Engaging Questions & Answers for Success

Master Class 10 Social Science: Engaging Questions & Answers for Success

Master Class 10 Maths: Engaging Questions & Answers for Success

Master Class 10 Science: Engaging Questions & Answers for Success

Trending doubts
What is the median of the first 10 natural numbers class 10 maths CBSE

The draft of the Preamble of the Indian Constitution class 10 social science CBSE

Who gave "Inqilab Zindabad" slogan?

Why is there a time difference of about 5 hours between class 10 social science CBSE

Write a letter to the principal requesting him to grant class 10 english CBSE

The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths




