Question

Which of the following is true:-
A. \[\dfrac{4}{5} < \dfrac{7}{9}\]
B. \[\dfrac{5}{9} < \dfrac{3}{10}\]
C. \[\dfrac{14}{15} < \dfrac{8}{14}\]
D. \[\dfrac{6}{22} > \dfrac{5}{21}\]

Answer 1

HINT:- We will firstly make the denominators of these fractions similar by taking the L.C.M. of their denominators one by one.

Complete step by step answer:
\[\dfrac{4}{5}\ and\dfrac{7}{9}\]

L.C.M. of 5 and 9

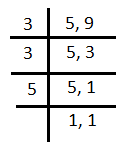
L.C.M. of 5 and 9 = \[3\times 3\times 5\] = 45
\[\dfrac{5}{9}and\dfrac{3}{10}\]

L.C.M. of 9 and 10

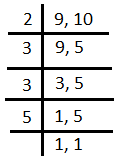
L.C.M. of 9 and 10 = \[2\times 3\times 3\times 5\] = 90
\[\dfrac{14}{15}and\dfrac{8}{14}\]

L.C.M. of 15 and 14

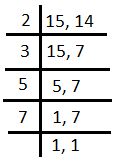
L.C.M. of 15 and 14 = \[2\times 3\times 5\times 7\] = 210
\[\dfrac{6}{22}and\dfrac{5}{21}\]

L.C.M. of 22 and 21

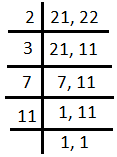
L.C.M. of 21 and 22 = \[2\times 3\times 7\times 11\] = 462

Let us solve the question now.
Let us check the first option:-
A. \[\dfrac{4}{5}<\dfrac{7}{9}\]
We know that the L.C.M. of the denominators of this fraction is 45.
Let us now make the denominators the same.
\[\dfrac{4\times 9}{5\times 9}=\dfrac{36}{45}\]
\[\dfrac{5\times 7}{9\times 5}=\dfrac{35}{45}\]
Hence, we can see that 36 is greater than 35, so \[\dfrac{\text{36}}{45}>\dfrac{35}{45}\] .
which means that \[~\dfrac{4}{5}>\dfrac{7}{9}\] .
Hence, this is a wrong option.

B. \[\dfrac{5}{9}<\dfrac{3}{10}\]
We know that the L.C.M. of the denominators of this fraction is 90.
Let us now make the denominators the same.
\[\dfrac{5\times 10}{9\times 10}=\dfrac{50}{90}\]
\[\dfrac{3\times 9}{10\times 9}=\dfrac{27}{90}\]
Hence, we can see that 50 is greater than 27, so \[\dfrac{\text{50 }}{90}>\dfrac{27}{90}\] .
which means that \[~\dfrac{5}{9}>\dfrac{3}{10}\] .
Hence, this is a wrong option.

C. \[\dfrac{14}{15}<\dfrac{8}{14}\]
We know that the L.C.M. of the denominators of this fraction is 210.
Let us now make the denominators the same.
\[\dfrac{14\times 14}{15\times 14}=\dfrac{196}{210}\]
\[\dfrac{8\times 15}{14\times 15}=\dfrac{120}{210}\]
Hence, we can see that 196 is greater than 120, so \[\dfrac{196\text{ }}{210}>\text{ }\dfrac{120}{210}\] .
This means that \[~\dfrac{14}{15}>\dfrac{8}{14}\] .
Hence, this is also a wrong option.

D. \[\dfrac{6}{22}>\dfrac{5}{21}\]
We know that the L.C.M. of the denominators of this fraction is 462.
Let us now make the denominators the same.
\[\dfrac{6\times 21}{22\times 21}=\dfrac{126}{462}\]
\[\dfrac{5\times 22}{22\times 21}=\dfrac{110}{462}\]
Hence, we can see that 126 is greater than 110, so \[\dfrac{126\text{ }}{462}>\text{ }\dfrac{110}{462}\] .
This means that \[~\dfrac{6}{22}>\text{ }\dfrac{5}{21}\] .
Hence, this is the correct option.

Therefore, the answer of this question is (D)

NOTE:- One must do all the calculations very carefully in this question. Also, must know how to calculate the L.C.M. of given numbers.
And not only in this question, the student should be very careful while solving any such question as any mistake in the calculations can make the answer wrong.