Question

Which of the following is the shadow of a two meter high post on a horizontal plane through its foot, when the altitude of the sun is ${30^ \circ }?$
A. $3\sqrt 3 m$
B. $\sqrt 7 m$
C. $2\sqrt 3 m$
D. $\dfrac{1}{{\sqrt 3 }}m$

Answer 1

Hint:First we have to draw the image according to the data given in the question. Here we have the length of the foot or base. We will use the trigonometric functions to solve this question. We know that the value of $\tan {30^ \circ } = \dfrac{1}{{\sqrt 3 }}$, also we know that $\tan \theta $ can be written as the ratio of $\dfrac{p}{b}$ , where $p$ is the perpendicular and $b$ is the base.

Complete step by step answer:
Let us first draw the diagram ;

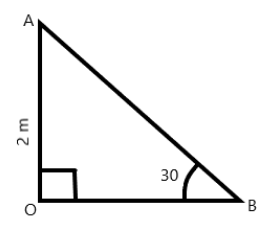
In the above triangle we have assumed $OA$ to be the height of the post and $OB$ to be the length of the shadow of the post. Let us assume angle $B$ to be the angle of the altitude of the Sun i.e. ${30^ \circ }$. From the above figure, we have perpendicular i.e.
$OA = 2m$
And, the base is
$OB$.
So, we can write,
$\tan \theta = \dfrac{p}{b} = \dfrac{{OA}}{{OB}}$
So from the above figure, we can write:
$\tan {30^ \circ } = \dfrac{1}{{\sqrt 3 }}$
By putting the above value of tangent, in the formula we have:
$ \Rightarrow \dfrac{{OA}}{{OB}} = \dfrac{1}{{\sqrt 3 }}$
We can put the value of OA:
$ \Rightarrow \dfrac{2}{{OB}} = \dfrac{1}{{\sqrt 3 }}$
By cross multiplication, it gives
$\therefore OB = 2\sqrt 3 m$

Hence the correct option is C.

Note:This question is related to height and distance. So our concept of height should be cleared. Height is a measure of vertical distance, or vertical extent. So if we use the term to describe the vertical position, the height is more often called altitude. Key point here is that in such height and distance based problems the trigonometric ratio of $\tan \theta $ is most frequently used, so we should align the line in this direction only while solving questions of this kind. We should always remember the basic trigonometric ratios formula line since it is the ratio of perpendicular and hypotenuse. We can write it as $\sin \theta = \dfrac{p}{h}$.