Question

Which of the following is the graph of $ y=\left| x-1 \right|+\left| x-3 \right| $ ? \[\]
A.

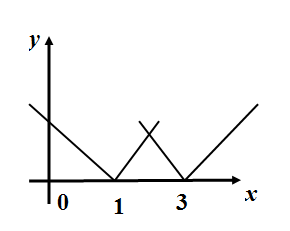
B.

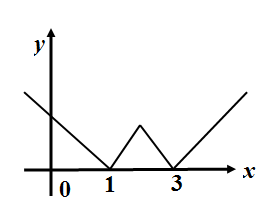
C.

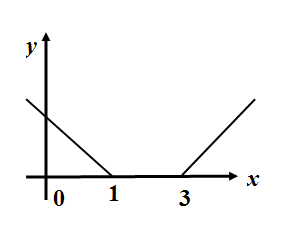
D.

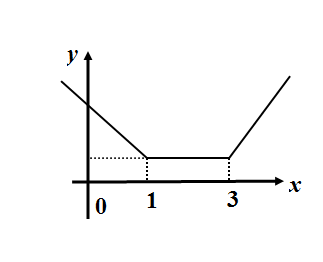
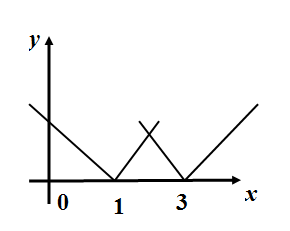
Answer 1

Hint: We recall the definition modulus function $ \left| x \right| $ which is piecewise defined with breaking point $ x=0 $ . We see in the given function $ y=\left| x-1 \right|+\left| x-3 \right| $ we have two break points that is $ x=1,x=3 $ . We find the definition of the function in the intervals $ \left( -\infty ,1 \right),\left[ 1,3 \right],\left( 3,\infty \right) $ and try to guess the function.


Complete step by step answer:
We know that of absolute value function of modulus function denoted as $ \left| x \right| $ returns a non-negative value without regard for the input of the functions. It is defined in piecewise manner as;
\[\left| x \right|=\left\{ \begin{matrix}
   -x & \text{if } x < 0\text{ } \\
   x & \text{if }x\ge 0 \\
\end{matrix} \right.\]
We see that the function has break point at $ x=0 $ which means the absolute value function has different definition for $ x\in \left( -\infty ,0 \right) $ and for $ x\in \left[ 0,\infty \right) $ . If we define an absolute value function $ \left| x-a \right| $ for any positive real number $ a $ then $ a $ will be the break point since $ \left| x-a \right| $ has to return non-negative outputs and for that we have to define the function as
\[\left| x-a \right|=\left\{ \begin{matrix}
   a-x & \text{if }x < a\text{ } \\
   x-a & \text{if }x\ge a \\
\end{matrix} \right.\]
We are given the following function in the question
\[y=\left| x-1 \right|+\left| x-3 \right|\]
We see that we are given two absolute value functions $ \left| x-1 \right|,\left| x-3 \right| $ and we have 2 break points $ x=1,3 $ for the piecewise wise definition. So we need to define the given function $ y $ in the intervals $ \left( -\infty ,1 \right),\left[ 1,3 \right],\left( 3,\infty \right) $ .
We have in the interval $ \left( -\infty ,1 \right) $ the function $ \left| x-1 \right|=1-x $ since $ x < 1 $ for all $ x\in \left( -\infty ,1 \right) $ . We also have $ \left| x-1 \right|=3-x $ since $ x < 3 $ for all $ x\in \left( -\infty ,1 \right) $ . So the given function in the interval $ \left( -\infty ,1 \right) $ can be defined as
\[\begin{align}
  & y=1-x+3-x \\
 & \Rightarrow y=-2x+4 \\
\end{align}\]
We see that the above equation is an equation of line with negative slope. Let us check the interval $ \left[ 1,3 \right] $ . Since $ x\ge 1 $ for all $ x\in \left[ 1,3 \right] $ we have $ \left| x-1 \right|=x-1 $ and since $ x\le 3 $ for all $ x\in \left[ 1,3 \right] $ we have $ \left| x-3 \right|=3-x $ . So the given function in the interval $ \left[ 1,3 \right] $ can be defined as
 \[\begin{align}
  & y=x-1+3-x \\
 & \Rightarrow y=2 \\
\end{align}\]
So the above equation is a line parallel to $ x- $ axis. . Let us check the interval $ \left( 3,\infty \right) $ . Since $ x\ge 1 $ for all $ x\in \left( 3,\infty \right) $ we have $ \left| x-1 \right|=x-1 $ and since $ x>3 $ for all $ x\in \left( 3,\infty \right) $ we have $ \left| x-3 \right|=x-3 $ . So the given function in the interval $ \left( 3,\infty \right) $ can be defined as
 \[\begin{align}
  & y=x-1+x-3 \\
 & \Rightarrow y=2x-4 \\
\end{align}\]
We see that the above equation is an equation of line with negative slope. We see at the break points $ x=1,3 $ the function values are
\[\begin{align}
  & \text{At }x=1:y=-2x+4=-2\left( 1 \right)+4=-2+4=2 \\
 & \text{At }x=3:\text{ }y=2x-4=2\left( 3 \right)-4=6-4=2 \\
\end{align}\]
So the give function is a continuous function but a decreasing line in $ \left( -\infty ,1 \right) $ , a parallel line above a distance of 2 from $ x- $ axis in $ \left[ 1,3 \right] $ and an increasing line in $ \left( 3,\infty \right) $ . We check the options and find the correct plot to be in D. \[\]

Note:
 We note that the general equation of line with slope and intercept form is given as $ y=mx+c $ where $ m $ is the slope and $ c $ is the $ y- $ intercept. If $ m $ is positive we get an increasing line, if $ m $ is negative we get a deceasing line and if $ m=0 $ we get a line parallel to $ x- $ axis. We can find the break points in $ \left| x+a \right| $ by converting it to $ \left| x-\left( -a \right) \right| $ .