Question

Which of the following is not an acute triangle?
A)

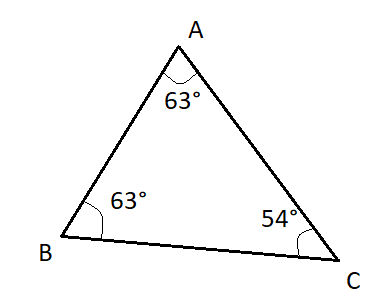
B)

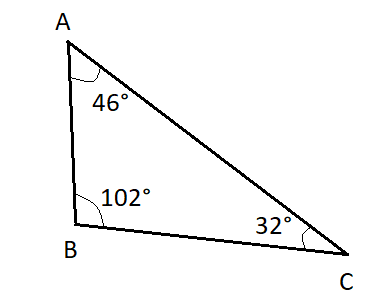
C)

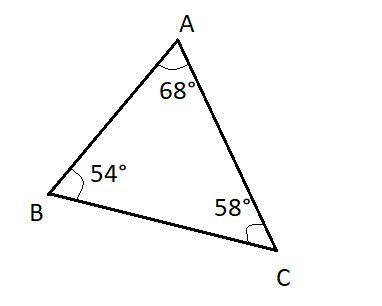
D)

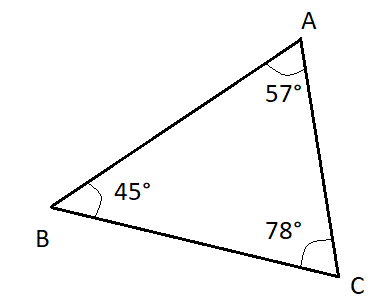
Answer 1

Hint: We have to find the acute angle triangle. In case of an acute angle triangle, the measure of internal angles of the triangle will always be less than \[{90^ \circ }\]. So, we can conclude that
\[\angle A,\angle B,\angle C \leqslant {90^ \circ }\]. We can solve the sum by carefully looking at the diagrams.

Complete step by step solution:
The sum of measure of all the three angles of the triangle shall be \[{180^ \circ }\]. Triangles can be classified into three types on the basis of their Angles:
Acute angled triangle- In this type of triangle, all the angles in the triangle measure less than \[{90^ \circ }\] E.g. \[{45^ \circ }\], \[{60^ \circ }\], \[{75^ \circ }\].
Right angled triangle - In this type of triangle one of the three angles in the triangle measures \[{90^ \circ }\] E.g. \[{90^ \circ }\], \[{45^ \circ }\], \[{45^ \circ }\].
Obtuse angled triangle - In this type of triangle one of the three Angles of a triangle measures more than \[{90^ \circ }\] E.g. \[{120^ \circ }\], \[{30^ \circ }\], \[{30^ \circ }\].
We can solve the sum by identifying whether any angle if more than \[{90^ \circ }\] as follows:
In the case of Option (A), (C) and (D), all the three angles of the triangle are less than \[{90^ \circ }\]. Hence, they all are acute triangles.
However, in the case of Option (B), \[m\angle B = {102^ \circ }\] which is more than \[{90^ \circ }\]. Hence, it is not an acute triangle; rather it is an obtuse triangle.

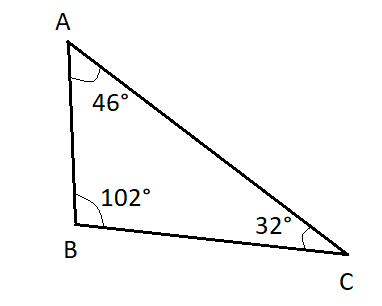
Therefore, Option (B) is the correct answer.

Note:
Some important properties of acute triangle are given below:
All equilateral triangles are acute triangles. An equilateral triangle has three sides of equal length and three equal angles of \[{60^ \circ }\].
Acute triangles can be isosceles, equilateral, or scalene.
The longest side of an acute triangle is opposite the largest angle.