Question

Which of the following is anti aromatic in nature
A.

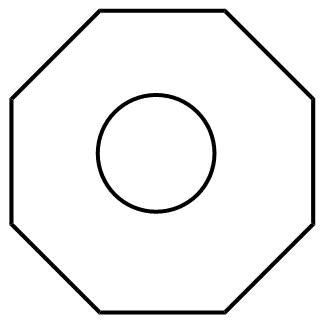
C.

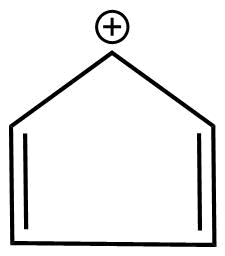
D.

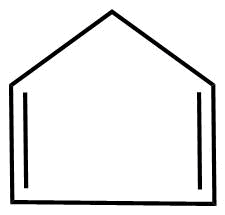
E.

Answer 1

Hint: A compound which has planar conjugated cyclic system and contains $4n$ pi-electrons which are destabilized by resonance are known as anti aromatic compounds .
Complete step by step answer:
We need four criterias to define Aromaticity and no exceptions are allowed.
1. the molecule has to be cyclic
2. Every atom in the ring has to be in conjugation, or every atom should have a p orbital.
3. the molecule should follow huckle’s rule for aromaticity
\[4n + 2\]
Where, $n$ is an integer
If it does not follow huckel's rule, check for $4n$ rule, if it satisfies this rule, then the molecule is non aromatic.
Where, $n$ is an integer
4. The molecule should be planar in nature.
Now, let us review the options one by one by checking off every point.
A.
1. The molecules are cyclic.
2. Every atom in the ring is in conjugation
3.It does not obey huckel's rule
But it does obey $4n$ rule
Where, $n = 2$
3. It is planar in nature.
Hence, the molecule is non-aromatic.
B.
1. The molecules are cyclic.
2. Every atom in the ring is not conjugation due to the positive charge there is discontinuation .
3.It does not obey huckel's rule
3. It is planar in nature.
Hence, the molecule is antiaromatic.
C. 1. The molecules are cyclic.
2. Every atom in the ring is in conjugation
3.It does not obey huckel's rule
But it does obey $4n$ rule
Where, $n = 2$
3. It is planar in nature.
Hence, the molecule is non-aromatic.
D.
1. The molecules are cyclic.
2. Every atom in the ring is in conjugation
3.It does obey huckel's rule
Where, $n = 2$
3. It is planar in nature.
Hence, the molecule is aromatic.

So, the correct answer is Option B.

Note: Compounds which do not obey Huckel’s rule are termed as anti aromatic compounds and are not stable compounds .They are even less stable than the corresponding non-planar systems.