
Which of the following has the greatest number of atoms?
A. ${\text{1}}\,{\text{g}}$ of butane $\left( {{{\text{C}}_{\text{4}}}{{\text{H}}_{{\text{10}}}}} \right)$
B. ${\text{1}}\,{\text{g}}$ of nitrogen $\left( {{{\text{N}}_2}} \right)$
C. ${\text{1}}\,{\text{g}}$ of silver $\left( {{\text{Ag}}} \right)$
D. ${\text{1}}\,{\text{g}}$ of water $\left( {{{\text{H}}_2}{\text{O}}} \right)$
Answer
582.6k+ views
Hint: According to the Avogadro, one mole of any substance have $\,6.02 \times {10^{23}}$ atoms, ions, or molecules. This number $\,6.02 \times {10^{23}}$ is known as Avogadro number. The total number of atoms can be determined by multiplying the moles of a substance with Avogadro number.
Step by step answer: The number of moles in a substance is determined by using the mole formula which is as follows:
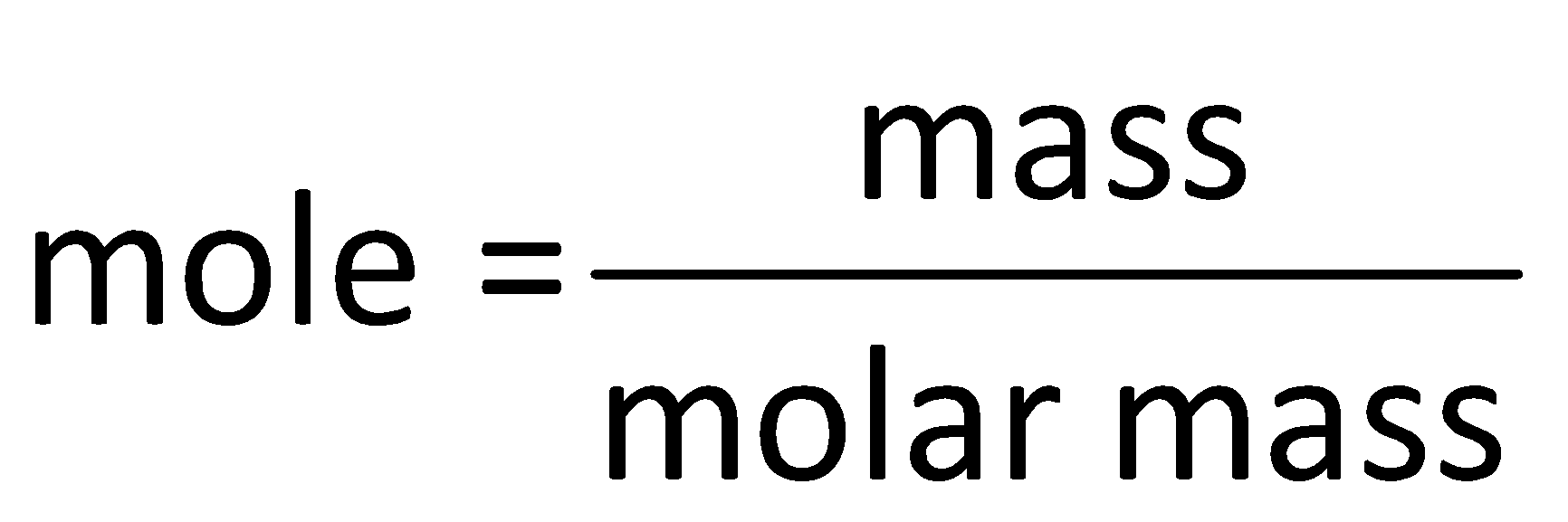
Determine the mole in ${\text{1}}\,{\text{g}}$ of butane as follows:
Substitute ${\text{1}}\,{\text{g}}$ for mass and $58\,{\text{g/mol}}$ for molar mass.
${\text{mole}}\,\,{\text{of }}{{\text{C}}_4}{{\text{H}}_{10}}{\text{ = }}\,\dfrac{{{\text{1 g}}}}{{{\text{58 g/mol}}}}$
${\text{mole}}\,\,{\text{of }}{{\text{C}}_4}{{\text{H}}_{10}}{\text{ = }}\,{\text{0}}{\text{.017}}\,{\text{mol}}$
Multiply the mole of butane with Avogadro number to determine the total number of molecules.
${\text{Molecules}}\,{\text{of }}{{\text{C}}_4}{{\text{H}}_{10}}{\text{ = }}\,{\text{0}}{\text{.017}}\,{\text{mol}} \times {\text{6}}{\text{.02}} \times {\text{1}}{{\text{0}}^{23}}{\text{molecules/mol}}$
${\text{Molecules}}\,\,{\text{of }}{{\text{C}}_4}{{\text{H}}_{10}}{\text{ = }}\,1.04 \times {\text{1}}{{\text{0}}^{22}}$
So, the number of molecules in ${\text{1}}\,{\text{g}}$of butane is $1.04 \times {\text{1}}{{\text{0}}^{22}}$.
One molecule of butane has $14$atoms. So, the total number atoms are as follows:
\[1.04 \times {\text{1}}{{\text{0}}^{22}} \times {\text{1}}4\]
\[14.6 \times {\text{1}}{{\text{0}}^{22}}{\text{atoms}}\]
So, the number of atoms in ${\text{1}}\,{\text{g}}$ of butane is\[14.6 \times {\text{1}}{{\text{0}}^{22}}\].
Determine the mole in ${\text{1}}\,{\text{g}}$ of nitrogen as follows:
Substitute ${\text{1}}\,{\text{g}}$ for mass and $14\,{\text{g/mol}}$ for molar mass.
${\text{mole}}\,\,{\text{of }}{{\text{N}}_2}{\text{ = }}\,\dfrac{{{\text{1 g}}}}{{{\text{14 g/mol}}}}$
${\text{mole}}\,\,{\text{of }}{{\text{N}}_2}{\text{ = }}\,{\text{0}}{\text{.071}}\,{\text{mol}}$
Multiply the mole of nitrogen with Avogadro number to determine the total number of molecules.
${\text{molecules}}\,\,{\text{of }}{{\text{N}}_2}{\text{ = }}\,{\text{0}}{\text{.071}}\,{\text{mol}} \times {\text{6}}{\text{.02}} \times {\text{1}}{{\text{0}}^{23}}{\text{molecules/mol}}$
${\text{molecules}}\,\,{\text{of }}{{\text{N}}_2}{\text{ = }}\,4.{\text{3}} \times {\text{1}}{{\text{0}}^{22}}$
So, the number of molecules in ${\text{1}}\,{\text{g}}$ of nitrogen is $4.3 \times {\text{1}}{{\text{0}}^{22}}$.
One molecule of nitrogen has $2$atoms.
$ = 4.3 \times {\text{1}}{{\text{0}}^{22}} \times 2$
$ = 8.6 \times {\text{1}}{{\text{0}}^{22}}$
So, the number of atoms in ${\text{1}}\,{\text{g}}$ of nitrogen is $8.6 \times {\text{1}}{{\text{0}}^{22}}$.
Determine the mole in ${\text{1}}\,{\text{g}}$ of silver as follows:
Substitute ${\text{1}}\,{\text{g}}$ for mass and $108\,{\text{g/mol}}$ for molar mass.
${\text{mole}}\,\,{\text{of Ag}}\,{\text{ = }}\,\,\dfrac{{{\text{1 g}}}}{{108\,{\text{g/mol}}}}$
${\text{mole}}\,\,{\text{of Ag}}\,{\text{ = }}\,\,{\text{9}}{\text{.259}} \times {\text{1}}{{\text{0}}^{ - 3}}\,{\text{mol}}$
Multiply the mole of silver with Avogadro number to determine the total number of molecules.
${\text{molecules}}\,\,{\text{of Ag}}\,{\text{ = }}\,\,{\text{9}}{\text{.259}} \times {\text{1}}{{\text{0}}^{ - 3}}\,{\text{mol}} \times {\text{6}}{\text{.02}} \times {\text{1}}{{\text{0}}^{23}}{\text{molecules/mol}}$
${\text{molecules}}\,{\text{of Ag}}\,{\text{ = }}\,\,0.55 \times {\text{1}}{{\text{0}}^{22}}$
One molecule of silver has one atom.
${\text{Atoms}}\,{\text{of Ag}}\,{\text{ = }}\,\,1\, \times 0.55 \times {\text{1}}{{\text{0}}^{22}}$
${\text{Atoms}}\,{\text{of Ag}}\,{\text{ = }}\,0.55 \times {\text{1}}{{\text{0}}^{22}}$
So, the number of atoms in ${\text{1}}\,{\text{g}}$ of silver is $0.55 \times {\text{1}}{{\text{0}}^{22}}$.
Determine the mole in ${\text{1}}\,{\text{g}}$ of water as follows:
Substitute ${\text{1}}\,{\text{g}}$ for mass and $18\,{\text{g/mol}}$ for molar mass.
${\text{mole}}\,\,{\text{of }}{{\text{H}}_2}{\text{O}}\,{\text{ = }}\,\,\dfrac{{{\text{1 g}}}}{{18\,{\text{g/mol}}}}$
${\text{mole}}\,\,{\text{of }}{{\text{H}}_2}{\text{O}}\,{\text{ = }}\,\,0.055\,{\text{mol}}$
Multiply the mole of water with Avogadro number to determine the total number of molecules.
\[{\text{molecules}}\,\,{\text{of }}{{\text{H}}_2}{\text{O}}\,{\text{ = }}\,\,0.055\,{\text{mol}} \times {\text{6}}{\text{.02}} \times {\text{1}}{{\text{0}}^{23}}{\text{molecules/mol}}\]
${\text{molecules}}\,\,{\text{of }}{{\text{H}}_2}{\text{O}}\,\,{\text{ = }}\,\,3.3 \times {\text{1}}{{\text{0}}^{22}}$
So, the number of molecules in ${\text{1}}\,{\text{g}}$ of water is $3.3 \times {\text{1}}{{\text{0}}^{22}}$.
One molecule of water has $3$atoms.
No. of atoms $ = 3 \times 3.3 \times {\text{1}}{{\text{0}}^{22}}$
No. of atoms $ = 9.9 \times {\text{1}}{{\text{0}}^{22}}{\text{atoms}}$
So, the number of atoms in ${\text{1}}\,{\text{g}}$ of water is$9.9 \times {\text{1}}{{\text{0}}^{22}}$.
${\text{1}}\,{\text{g}}$ of butane has the highest number of moles so, option (B), (C), (D) are incorrect.
Therefore, option (A) ${\text{1}}\,{\text{g}}$ of butane$\left( {{{\text{C}}_{\text{4}}}{{\text{H}}_{{\text{10}}}}} \right)$, is correct.
Note: Atomicity also denotes the number of atoms in a substance. Here, the gram amount of each substance is given so, the total number of atoms is determined by multiplying the moles with Avogadro's number and number of atoms in one molecule. If the gram amount is not given the total number of atoms can be determined by adding the number of atoms of a substance.
Step by step answer: The number of moles in a substance is determined by using the mole formula which is as follows:
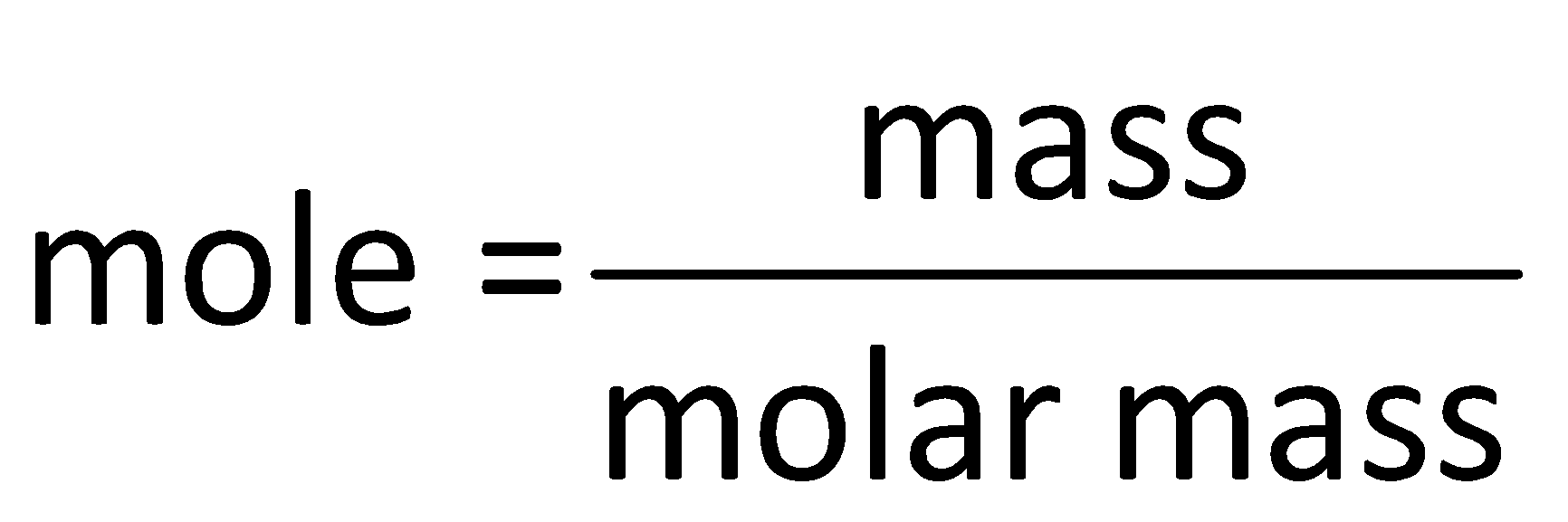
Determine the mole in ${\text{1}}\,{\text{g}}$ of butane as follows:
Substitute ${\text{1}}\,{\text{g}}$ for mass and $58\,{\text{g/mol}}$ for molar mass.
${\text{mole}}\,\,{\text{of }}{{\text{C}}_4}{{\text{H}}_{10}}{\text{ = }}\,\dfrac{{{\text{1 g}}}}{{{\text{58 g/mol}}}}$
${\text{mole}}\,\,{\text{of }}{{\text{C}}_4}{{\text{H}}_{10}}{\text{ = }}\,{\text{0}}{\text{.017}}\,{\text{mol}}$
Multiply the mole of butane with Avogadro number to determine the total number of molecules.
${\text{Molecules}}\,{\text{of }}{{\text{C}}_4}{{\text{H}}_{10}}{\text{ = }}\,{\text{0}}{\text{.017}}\,{\text{mol}} \times {\text{6}}{\text{.02}} \times {\text{1}}{{\text{0}}^{23}}{\text{molecules/mol}}$
${\text{Molecules}}\,\,{\text{of }}{{\text{C}}_4}{{\text{H}}_{10}}{\text{ = }}\,1.04 \times {\text{1}}{{\text{0}}^{22}}$
So, the number of molecules in ${\text{1}}\,{\text{g}}$of butane is $1.04 \times {\text{1}}{{\text{0}}^{22}}$.
One molecule of butane has $14$atoms. So, the total number atoms are as follows:
\[1.04 \times {\text{1}}{{\text{0}}^{22}} \times {\text{1}}4\]
\[14.6 \times {\text{1}}{{\text{0}}^{22}}{\text{atoms}}\]
So, the number of atoms in ${\text{1}}\,{\text{g}}$ of butane is\[14.6 \times {\text{1}}{{\text{0}}^{22}}\].
Determine the mole in ${\text{1}}\,{\text{g}}$ of nitrogen as follows:
Substitute ${\text{1}}\,{\text{g}}$ for mass and $14\,{\text{g/mol}}$ for molar mass.
${\text{mole}}\,\,{\text{of }}{{\text{N}}_2}{\text{ = }}\,\dfrac{{{\text{1 g}}}}{{{\text{14 g/mol}}}}$
${\text{mole}}\,\,{\text{of }}{{\text{N}}_2}{\text{ = }}\,{\text{0}}{\text{.071}}\,{\text{mol}}$
Multiply the mole of nitrogen with Avogadro number to determine the total number of molecules.
${\text{molecules}}\,\,{\text{of }}{{\text{N}}_2}{\text{ = }}\,{\text{0}}{\text{.071}}\,{\text{mol}} \times {\text{6}}{\text{.02}} \times {\text{1}}{{\text{0}}^{23}}{\text{molecules/mol}}$
${\text{molecules}}\,\,{\text{of }}{{\text{N}}_2}{\text{ = }}\,4.{\text{3}} \times {\text{1}}{{\text{0}}^{22}}$
So, the number of molecules in ${\text{1}}\,{\text{g}}$ of nitrogen is $4.3 \times {\text{1}}{{\text{0}}^{22}}$.
One molecule of nitrogen has $2$atoms.
$ = 4.3 \times {\text{1}}{{\text{0}}^{22}} \times 2$
$ = 8.6 \times {\text{1}}{{\text{0}}^{22}}$
So, the number of atoms in ${\text{1}}\,{\text{g}}$ of nitrogen is $8.6 \times {\text{1}}{{\text{0}}^{22}}$.
Determine the mole in ${\text{1}}\,{\text{g}}$ of silver as follows:
Substitute ${\text{1}}\,{\text{g}}$ for mass and $108\,{\text{g/mol}}$ for molar mass.
${\text{mole}}\,\,{\text{of Ag}}\,{\text{ = }}\,\,\dfrac{{{\text{1 g}}}}{{108\,{\text{g/mol}}}}$
${\text{mole}}\,\,{\text{of Ag}}\,{\text{ = }}\,\,{\text{9}}{\text{.259}} \times {\text{1}}{{\text{0}}^{ - 3}}\,{\text{mol}}$
Multiply the mole of silver with Avogadro number to determine the total number of molecules.
${\text{molecules}}\,\,{\text{of Ag}}\,{\text{ = }}\,\,{\text{9}}{\text{.259}} \times {\text{1}}{{\text{0}}^{ - 3}}\,{\text{mol}} \times {\text{6}}{\text{.02}} \times {\text{1}}{{\text{0}}^{23}}{\text{molecules/mol}}$
${\text{molecules}}\,{\text{of Ag}}\,{\text{ = }}\,\,0.55 \times {\text{1}}{{\text{0}}^{22}}$
One molecule of silver has one atom.
${\text{Atoms}}\,{\text{of Ag}}\,{\text{ = }}\,\,1\, \times 0.55 \times {\text{1}}{{\text{0}}^{22}}$
${\text{Atoms}}\,{\text{of Ag}}\,{\text{ = }}\,0.55 \times {\text{1}}{{\text{0}}^{22}}$
So, the number of atoms in ${\text{1}}\,{\text{g}}$ of silver is $0.55 \times {\text{1}}{{\text{0}}^{22}}$.
Determine the mole in ${\text{1}}\,{\text{g}}$ of water as follows:
Substitute ${\text{1}}\,{\text{g}}$ for mass and $18\,{\text{g/mol}}$ for molar mass.
${\text{mole}}\,\,{\text{of }}{{\text{H}}_2}{\text{O}}\,{\text{ = }}\,\,\dfrac{{{\text{1 g}}}}{{18\,{\text{g/mol}}}}$
${\text{mole}}\,\,{\text{of }}{{\text{H}}_2}{\text{O}}\,{\text{ = }}\,\,0.055\,{\text{mol}}$
Multiply the mole of water with Avogadro number to determine the total number of molecules.
\[{\text{molecules}}\,\,{\text{of }}{{\text{H}}_2}{\text{O}}\,{\text{ = }}\,\,0.055\,{\text{mol}} \times {\text{6}}{\text{.02}} \times {\text{1}}{{\text{0}}^{23}}{\text{molecules/mol}}\]
${\text{molecules}}\,\,{\text{of }}{{\text{H}}_2}{\text{O}}\,\,{\text{ = }}\,\,3.3 \times {\text{1}}{{\text{0}}^{22}}$
So, the number of molecules in ${\text{1}}\,{\text{g}}$ of water is $3.3 \times {\text{1}}{{\text{0}}^{22}}$.
One molecule of water has $3$atoms.
No. of atoms $ = 3 \times 3.3 \times {\text{1}}{{\text{0}}^{22}}$
No. of atoms $ = 9.9 \times {\text{1}}{{\text{0}}^{22}}{\text{atoms}}$
So, the number of atoms in ${\text{1}}\,{\text{g}}$ of water is$9.9 \times {\text{1}}{{\text{0}}^{22}}$.
${\text{1}}\,{\text{g}}$ of butane has the highest number of moles so, option (B), (C), (D) are incorrect.
Therefore, option (A) ${\text{1}}\,{\text{g}}$ of butane$\left( {{{\text{C}}_{\text{4}}}{{\text{H}}_{{\text{10}}}}} \right)$, is correct.
Note: Atomicity also denotes the number of atoms in a substance. Here, the gram amount of each substance is given so, the total number of atoms is determined by multiplying the moles with Avogadro's number and number of atoms in one molecule. If the gram amount is not given the total number of atoms can be determined by adding the number of atoms of a substance.
Recently Updated Pages
Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Master Class 11 Biology: Engaging Questions & Answers for Success

Trending doubts
One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

There are 720 permutations of the digits 1 2 3 4 5 class 11 maths CBSE

Discuss the various forms of bacteria class 11 biology CBSE

Draw a diagram of a plant cell and label at least eight class 11 biology CBSE

State the laws of reflection of light

Explain zero factorial class 11 maths CBSE




