Question

Which of the following do/does not reduce to unity?
This question has multiple correct options.
A) $\dfrac{{\sin \left( {180^\circ + A} \right)}}{{\tan \left( {180^\circ + A} \right)}}.\dfrac{{\cot \left( {90^\circ + A} \right)}}{{\tan \left( {90^\circ + A} \right)}}\dfrac{{\cos \left( {360^\circ - A} \right)\cos ecA}}{{\sin \left( { - A} \right)}}$
B) \[\dfrac{{\sin \left( { - A} \right)}}{{\sin \left( {180^\circ + A} \right)}} - \dfrac{{\tan \left( {90^\circ + A} \right)}}{{\cot A}} + \dfrac{{\cos A}}{{\sin \left( {90^\circ + A} \right)}}\]
C) $\dfrac{{\sin 24^\circ \cos 6^\circ - \sin 6^\circ \cos 24^\circ }}{{\sin 51^\circ \cos 69^\circ - \cos 51^\circ \sin 69^\circ }}$
D) $\dfrac{{\cos \left( {90^\circ + A} \right)\sec \left( { - A} \right)\tan \left( {180^\circ - A} \right)}}{{\sec \left( {360^\circ + A} \right)\sin \left( {180^\circ + A} \right)\cot \left( {90^\circ - A} \right)}}$

Answer 1

Hint:
We can simplify each of the given options. Firstly, we can simplify the angles by retaining the ratio for supplementary angles and by changing the ratio for complementary angles and assigning the signs by checking the quadrants. Then we can simplify by cancelling the common terms. The options that will cancel all the terms in the numerator and denominators will give the required options.

Complete step by step solution:
Consider the $1^{\text{st}}$ option
 $\dfrac{{\sin \left( {180^\circ + A} \right)}}{{\tan \left( {180^\circ + A} \right)}}.\dfrac{{\cot \left( {90^\circ + A} \right)}}{{\tan \left( {90^\circ + A} \right)}}\dfrac{{\cos \left( {360^\circ - A} \right)\cos ecA}}{{\sin \left( { - A} \right)}}$
Let $a = \dfrac{{\sin \left( {180^\circ + A} \right)}}{{\tan \left( {180^\circ + A} \right)}}.\dfrac{{\cot \left( {90^\circ + A} \right)}}{{\tan \left( {90^\circ + A} \right)}}\dfrac{{\cos \left( {360^\circ - A} \right)\cos ecA}}{{\sin \left( { - A} \right)}}$
On simplifying the angles, we get,
 \[ \Rightarrow a = \dfrac{{ - \sin \left( A \right)}}{{\tan \left( A \right)}}.\dfrac{{\tan \left( A \right)}}{{\cot \left( A \right)}}\dfrac{{\cos \left( A \right)\cos ecA}}{{ - \sin \left( A \right)}}\]
On cancelling the common terms, we get,
 \[ \Rightarrow a = \dfrac{{\cos \left( A \right)\cos ecA}}{{\cot \left( A \right)}}\]
We know that $\cot A = \dfrac{{\cos A}}{{\sin A}}$ and \[\cos ecA = \dfrac{1}{{\sin A}}\] . $ \Rightarrow \cot A = \cos A\operatorname{cosec} A$
 \[ \Rightarrow a = \dfrac{{\cos \left( A \right)\cos ecA}}{{\cos A\cos ecA}}\]
On cancelling the common terms, we get,
 \[ \Rightarrow a = 1\]
Therefore, option A reduces to unity.
Now we can consider option B.
Let \[b = \dfrac{{\sin \left( { - A} \right)}}{{\sin \left( {180^\circ + A} \right)}} - \dfrac{{\tan \left( {90^\circ + A} \right)}}{{\cot A}} + \dfrac{{\cos A}}{{\sin \left( {90^\circ + A} \right)}}\]
On simplifying the complementary and supplementary angles, we get,
 \[ \Rightarrow b = \dfrac{{ - \sin \left( A \right)}}{{ - \sin \left( A \right)}} - \dfrac{{ - \cot A}}{{\cot A}} + \dfrac{{\cos A}}{{ - \cos A}}\]
On cancelling the common terms, we get,
 \[ \Rightarrow b = 1 + 1 - 1\]
On simplification we get,
 \[ \Rightarrow b = 1\]
Therefore, option B also reduces to unity.
Now we can consider option C.
Let $c = \dfrac{{\sin 24^\circ \cos 6^\circ - \sin 6^\circ \cos 24^\circ }}{{\sin 51^\circ \cos 69^\circ - \cos 51^\circ \sin 69^\circ }}$
We know that $\sin A\cos B - \sin B\cos A = \sin \left( {A - B} \right)$ .So the numerator and denominator will become,
 $ \Rightarrow c = \dfrac{{\sin \left( {24^\circ - 6^\circ } \right)}}{{\sin \left( {51^\circ - 69^\circ } \right)}}$
On simplification we get,
 $ \Rightarrow c = \dfrac{{\sin \left( {18^\circ } \right)}}{{\sin \left( { - 18^\circ } \right)}}$
We know that $\sin \left( { - A} \right) = - \sin A$ .
 $ \Rightarrow c = \dfrac{{\sin \left( {18^\circ } \right)}}{{ - \sin \left( {18^\circ } \right)}}$
On cancelling the common terms, we get,
 $ \Rightarrow c = - 1$
Therefore, option C does not reduce to unity.
Now consider option D.
Let $d = \dfrac{{\cos \left( {90^\circ + A} \right)\sec \left( { - A} \right)\tan \left( {180^\circ - A} \right)}}{{\sec \left( {360^\circ + A} \right)\sin \left( {180^\circ + A} \right)\cot \left( {90^\circ - A} \right)}}$
On simplifying the complementary and supplementary angles, we get,
 $ \Rightarrow d = \dfrac{{\left( {\sin A} \right)\left( { - \sec A} \right)\left( { - \tan A} \right)}}{{\left( {\sec A} \right)\left( { - \sin A} \right)\left( {\tan A} \right)}}$
On cancelling the common terms, we get,
 $ \Rightarrow d = \dfrac{{\left( { - 1} \right)\left( { - 1} \right)}}{{\left( { - 1} \right)}}$
On simplification we get,
 $ \Rightarrow d = - 1$
Therefore, option D does not reduce to unity.
Thus, only option A and B reduces to unity.

So, the correct answer is options are option A and option B.

Note:
We must be familiar with the following trigonometric identities used in this problem.
 $\sin A\cos B - \sin B\cos A = \sin \left( {A - B} \right)$
 $\cot A = \dfrac{{\cos A}}{{\sin A}}$
 \[\cos ecA = \dfrac{1}{{\sin A}}\]
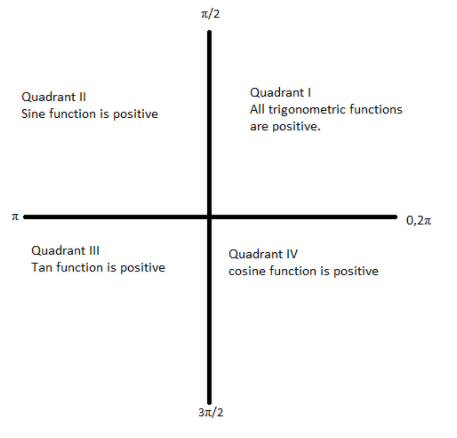
Adding $\pi $ or multiples of $\pi $ with the angle retains the ratio and adding $\dfrac{\pi }{2}$ or odd multiples of $\dfrac{\pi }{2}$ will change the ratio. While converting the angles we must take care of the sign of the ratio in its respective quadrant. In the $1^{\text{st}}$ quadrant all the trigonometric ratios are positive. In the $2^{\text{nd}}$ quadrant only sine and sec are positive. In the third quadrant, only tan and cot are positive and in the fourth quadrant, only cos and sec are positive. The following figure gives us an idea about the signs of different trigonometric functions. The angle measured in the counterclockwise direction is taken as positive and angle measured in the clockwise direction is taken as negative.